Testtheorie

Die Testtheorie umfasst Verfahren zur Überprüfung von statistischen Hypothesen, basierend auf Stichproben.

In der Regel hast Du bestimmte Vorstellungen und Vermutungen über Parameter und/oder Verteilungen der Grundgesamtheit. Diese möchtest Du mit Hilfe von Testverfahren überprüfen. Du weißt aber auch, dass sich die konkreten Realisierungen der Stichprobe sowohl aus den Parametern der Grundgesamtheit als auch aus Zufallseinflüssen zusammensetzen. Diese können in der Praxis nie ausgeschlossen werden.

Anwendung der Testtheorie

Angenommen, Du arbeitest in der Qualitätskontrolle einer Molkerei, die Joghurtbecher mit einem aufgedruckten Gewicht von 150 g befüllt. Natürlich kommen dabei leichte Gewichtsschwankungen um das eingestellte mittlere Gewicht vor. Diese sollten aber nicht systematisch sein. Ein zu hoch eingestelltes Gewicht bedeutet zusätzliche Kosten. Ein zu niedriges Gewicht beeinflusst die Kundenzufriedenheit negativ.

Täglich entnimmst Du daher aus der Herstellung eine Stichprobe. Damit überprüfst Du, ob das mittlere Gewicht der Tagesproduktion stimmt oder ob die Abfüllmaschine neu eingestellt werden muss.

Die Testtheorie liefert Dir Prüfverfahren, um diese Entscheidung statistisch mit einem bestimmten Signifikanzniveau α treffen zu können. Du berechnest je nach Test eine Prüfgröße aus Deinen Stichprobenwerten und vergleichst sie mit dem zu α gehörigen kritischen Bereich: Liegt die Prüfgröße im kritischen Bereich, so wird die Nullhypothese verworfen. Anderenfalls verwirfst Du sie nicht.

Die Grafik zeigt den kritischen Bereich blau schraffiert. Liegt die Prüfgröße also im nicht schraffierten Bereich, so wird die Nullhypothese nicht verworfen.

 

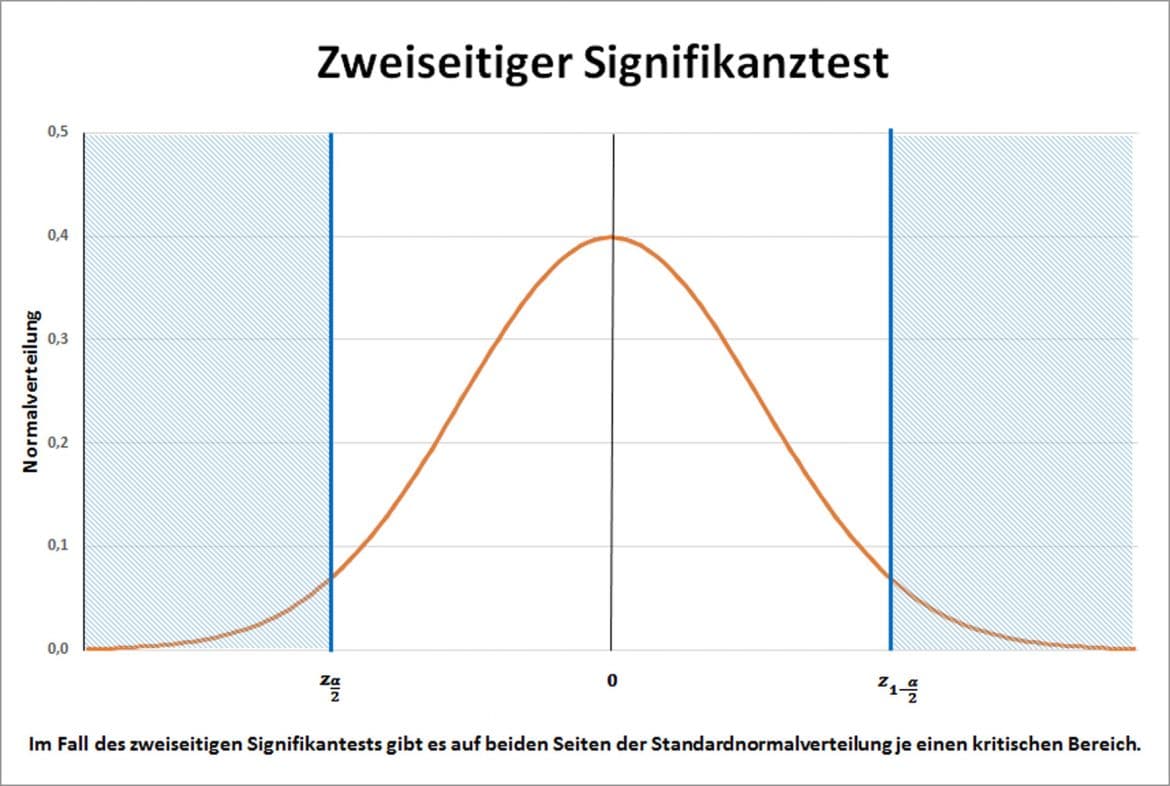
Das Testergebnis liefert Dir folgende Informationen:

• Wird die Nullhypothese aufgrund des Stichprobenergebnisses nicht verworfen, gibt es zum Signifikanzniveau α aus statistischer Sicht keinen Grund, sie als falsch anzusehen. Daraus darfst Du aber nicht schließen, dass sie richtig ist. Denn grundsätzlich lassen sich empirische Aussagen zwar falsifizieren, nicht aber verifizieren.
• Führt das Ergebnis aus der Stichprobe dagegen zum Verwerfen der Nullhypothese, so beträgt die Wahrscheinlichkeit dafür, dass diese Entscheidung falsch ist, .

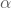Allgmeines Vorgehen beim statistischen Testen

Ein statistischer Test läuft allgemein in drei Schritten ab. Hier zeigen wir jeden dieser Schritte mit Deinem Molkereibeispiel.

1. Zunächst formulierst Du Deine Vermutung als Hypothese. Diese bezeichnet man als Nullhypothese H0. Dazu gehört die Alternativhypothese H1 und das Signifikanzniveau α.
   H0: Die Maschine ist richtig eingestellt. Das mittlere Abfüllgewicht liegt bei 150 g.
   H1: Die Maschine ist falsch eingestellt und es gibt systematische Abweichungen.
   Das Signifikanzniveau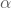 beträgt wie sehr oft 5%.
2. Du ziehst Deine Stichprobe und wertest sie aus.
   Dein Stichprobenmittelwert ergibt sich als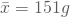 . Die Varianz der Stichprobe ist aufgrund von längerfristigen Stichproben als bekannt.
3. Du vergleicht Deine Testgröße mit dem kritischen Bereich und triffst die Testentscheidung.
   Du standardisierst Deinen Mittelwert und vergleichst ihn mit den hier kritischen Werten, die Du als die inverse Verteilungsfunktion der Standardnormalverteilung zum Niveau 2,5% und 97,5% erhältst.
   Liegt Deine Testgröße zwischen den beiden kritischen Werten, so wird die Nullhypothese nicht verworfen; liegt sie unterhalb des unteren oder oberhalb des oberen kritischen Wertes, so wird sie verworfen und Du schließt mit einem Signifikanzniveau von 5%, dass die Abfüllmaschine neu eingestellt werden muss.

Nach Durchführung des Tests kannst Du dann bei einem nicht signifikanten Testergebnis formulieren: Bei einem Signifikanzniveau von 5% gibt es keinen statistischen Grund anzunehmen, das Gewicht der Tagesproduktion stimme nicht mit dem aufgedruckten Gewicht überein.

Falls Du aufgrund des Testergebnisses auf systematische Abweichungen vom Füllgewicht schließt, liegt die Wahrscheinlichkeit für einen Fehlschluss bei 5%.

Bei dem hier betrachteten Beispiel handelt es sich um einen zweiseitigen Signifikanztest, da Du Abweichungen in beide Richtungen vermeiden wolltest.

Falls Du mit dem Test sicherstellen möchtest, dass ein bestimmter Wert nicht unter- oder überschritten wird, so führst Du einen einseitigen Test durch.