Gaußtest / z-Test

Gaußtest / z-Test

  • 26. Januar 2017
  • Posted by: Mika
Keine Kommentare

Möchtest Du anhand Deiner Stichprobe(n) Hypothesen über den oder die Mittelwerte der Grundgesamtheit prüfen, so kommt der Gaußtest als geeignetes Instrument in Frage. Um ihn anwenden zu können, musst Du die Varianz der Grundgesamtheit kennen und für die Stichprobe Normalverteilung annehmen können. Damit ist dieser Test für kleine Stichproben oft nicht anwendbar.

Einstichprobentest

Du hast eine Stichprobe, für die Du Normalverteilung unterstellen kannst und deren Varianz in der Grundgesamtheit bekannt ist. Du kannst für den Stichprobenmittelwert testen, ob er mit einem angenommenen Mittelwert der Grundgesamtheit vereinbar ist (zweiseitiger Test) oder ob es systematische Abweichungen nach oben oder nach unten gibt (einseitiger Test).

Stell Dir vor, Du als Delikatessenhändler möchtest für Deine Kunden als Aufmerksamkeit hochwertiges Olivenöl in Probefläschchen zu 150 ml beziehen. Von Deinem Abfüller weißt Du aus langjähriger Erfahrung, dass die Füllmenge einer Normalverteilung folgt, mit einer Standardabweichung von \sigma=1,5. Du lässt Dir eine Probelieferung von 120 Flaschen schicken und überprüfst anhand dieser Stichprobe, ob der Anbieter das Öl wie vereinbart abfüllt. Die mittlere Füllmenge der Stichprobe beträgt 149,8 ml.

Als erstes formulierst Du Deine Hypothesen. Wichtig ist Dir, dass die Füllmenge nicht zu gering ausfällt. Da Du nur den Alphafehler kontrollieren kannst, formulierst Du Deine Hypothese entgegengesetzt dazu als

    \begin{equation*} H_0: \mu \ge 150 \quad und \quad H_1: \mu < 150. \end{equation*}

Die Füllmenge ist normalverteilt – daher kannst Du den Stichprobenmittelwert standardisieren und diesen Wert z_{pr} mit dem kritischen Wert z_{kr} = 1,645 der Standardnormalverteilung zum Niveau \alpha=5\% vergleichen: Mit

    \begin{equation*} \frac { \bar x - \mu} { \frac {\sigma} {\sqrt n}}= \frac {149,8 - 150} {\frac {1,5} {\sqrt {120} }} = -1,46=z_{pr} > z_{kr} =-1,645 \end{equation*}

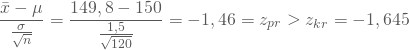
wird die Nullhypothese nicht verworfen. Dein Test liefert also zum Signifikanzniveau von 5\% keinen Anlass, an der ausreichenden Befüllung des Anbieters zu zweifeln. Die Grafik zeigt: dass Deine Prüfgröße im gelben Annahmebereich liegt und verdeutlicht so Deine Testentscheidung.

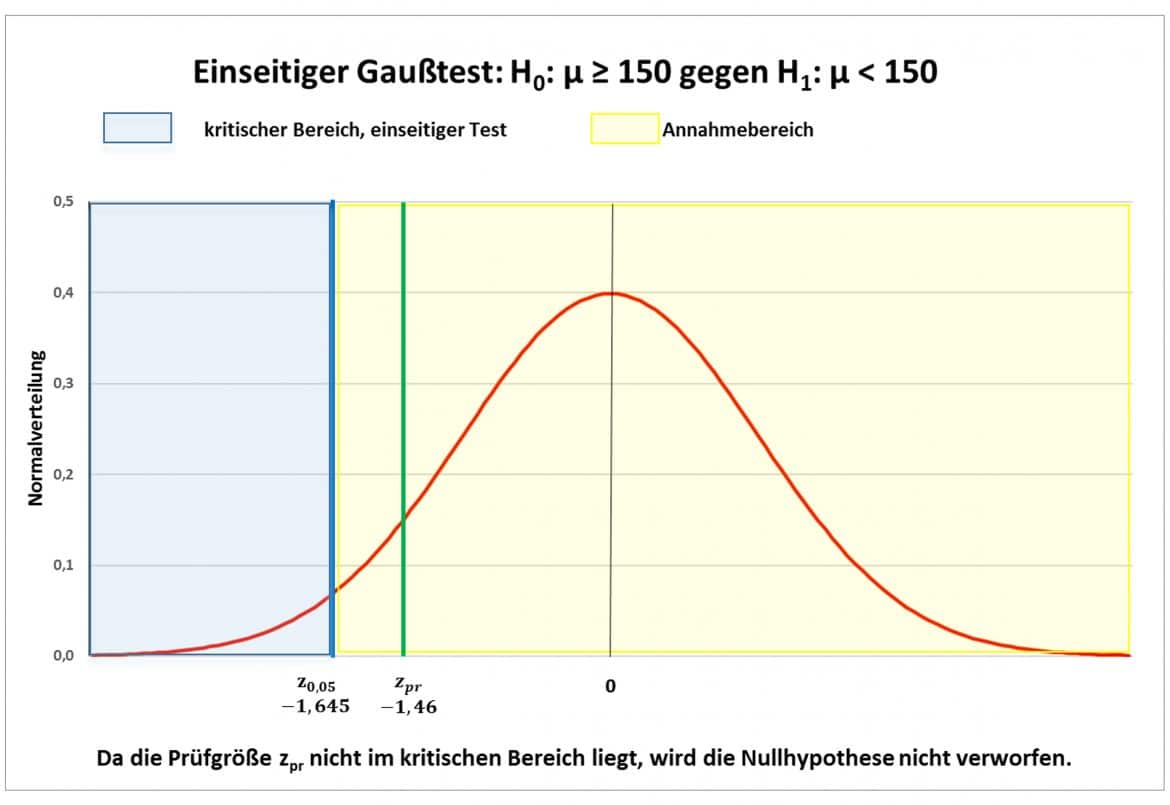
gausstest-einseitig

Zweistichprobentest für unverbundene Stichproben

Dir liegen zwei Stichproben vor, die beide zu normalverteilten Zufallsvariablen gehören und deren Varianzen der Grundgesamtheit Dir bekannt sind: Du kannst testen, ob die beiden Mittelwerte gleich sind oder ob es systematische Unterschiede gibt.

Nach ein paar Wochen ziehst Du zur Kontrolle wieder eine Stichprobe, diesmal vom Umfang n_2 = 100, die bei gleicher Standardabweichung diesmal eine mittlere Füllmenge von \bar x_2 = 150,8 liefert. Du möchtest jetzt testen, ob die Unterschiede zwischen der ersten und zweiten Stichprobe zufällig bedingt sind oder ob die Füllmenge tatsächlich angestiegen ist.

Die Differenz zwischen den beiden Stichprobenmittelwerten kannst Du als Realisation einer linear aus X_1 und X_2 zusammengesetzten Zufallsvariablen D = X_2 - X_1 betrachten, deren Erwartungswert (\mu_2 - \mu_1) ist und deren Varianz Du als

    \begin{equation*} \sigma^2_D = \frac {\sigma^2_2} {\sqrt {n_2}} + \frac {\sigma^2_1}{\sqrt {n_1}} \end{equation*}

berechnen kannst.

 

Du vermutest aufgrund der Stichprobenergebnisse, dass eventuell ein Anstieg der Füllmenge erfolgt ist, was einen positiven Wert der Zufallsvariablen D bedeutet, und möchtest vor allem den Fehler kontrollieren, ein signifikantes Ansteigen der Füllmenge nicht zu bemerken. Deine Hypothesen lauten daher:

    \begin{equation*} H_0: (\mu_2 - \mu_1) \le 0 \quad und \quad H_1: (\mu_2 - \mu_1) >0 \end{equation*}

Als Teststatistik dividierst Du die Differenz zwischen den Mittelwerten durch die Standardabweichung \sigma_D, um sie mit den z-Werten der Standardnormalverteilung vergleichbar zu machen. Du verwirfst die Nullhypothese, falls Dein Prüfwert den kritischen Wert zum Niveau (1-\alpha) = 95\% überschreitet.
Mit

    \begin{equation*} \frac {150,8 - 149,8} { \sqrt {\frac {1,5^2} {100}+ \frac {1,5^2} {120}} } = \frac {1} {\sqrt {0,04125}} = 4,92 = z_{pr} > z_{kr} =z_{0,95} = 1,645 \end{equation*}

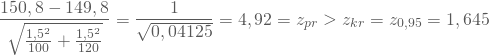
verwirfst Du Deine Nullhypothese, die mittlere Füllmenge zum zweiten Zeitpunkt sei kleiner oder gleich der ersten Stichprobe. Dein Stichprobenvergleich lässt also auf einen tatsächlich erfolgten Anstieg der Füllmenge schließen.

Zweistichprobentest für verbundene Stichproben

Für jedes i = 1 bis n liegen Paare von Messwerten vor, z.B. „vorher-nachher-Werte“, die die gleiche Varianz aufweisen und normalverteilt sind. Du kannst testen, ob die beiden Mittelwerte der Messungen gleich sind oder ob es systematische Abweichungen gibt.

Mit der im Zeitablauf angestiegenen Füllmenge kannst Du als Abnehmer zufrieden sein.

Aber es interessiert Dich doch, ob dieser angebliche Anstieg nicht vielleicht durch Messfehler zustande gekommen ist, und Du entschließt Dich, jedes Fläschchen der zweiten Stichprobe ein weiteres Mal zu messen. Damit hast Du für jede Flasche ein Paar von Messwerten (x_i,y_i) notiert, deren zugrundeliegende Zufallsvariablen X und Y beide einer Normalverteilung mit bekanntem \sigma = 1,5 folgen. Aus den Messpaaren kannst Du die Differenzen d_i = x_i-y_i sowie deren Mittelwert zu \bar d ermitteln. Falls kein Messfehler aufgetreten ist, ist der Mittelwert der beiden Stichproben in der Grundgesamtheit derselbe. Die Varianz von D ergibt sich als Summe der Varianzen von X und Y als 2 \cdot \sigma^2.

Testen der Nullhypothese

Du testest Deine Nullhypothese, der Mittelwert \mu von D sei Null:

    \begin{equation*} H_0: \mu = 0 \quad gegen \quad H_1: \mu \ne 0 \end{equation*}

Deine Teststatistik ergibt sich als standardisierter Mittelwert der d_i , \bar d = 0,4, und Du vergleichst sie mit den kritischen Werten auf beiden Seiten der Verteilung, jeweils zum Signifikanzniveau von \alpha/2. Deine Testentscheidung

    \begin{equation*} \frac {\bar d} { \sqrt { \frac {2\cdot \sigma^2} n } }= \frac {0,4} {0,2121} = 1,886 = z_{pr} < z_{kr} =z_{0,975}= 1,96 \end{equation*}

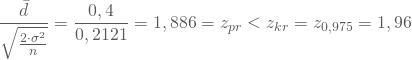
kann für den zweiseitigen Signifikanztest keine systematischen Abweichungen der beiden Stichprobenmittelwerte feststellen.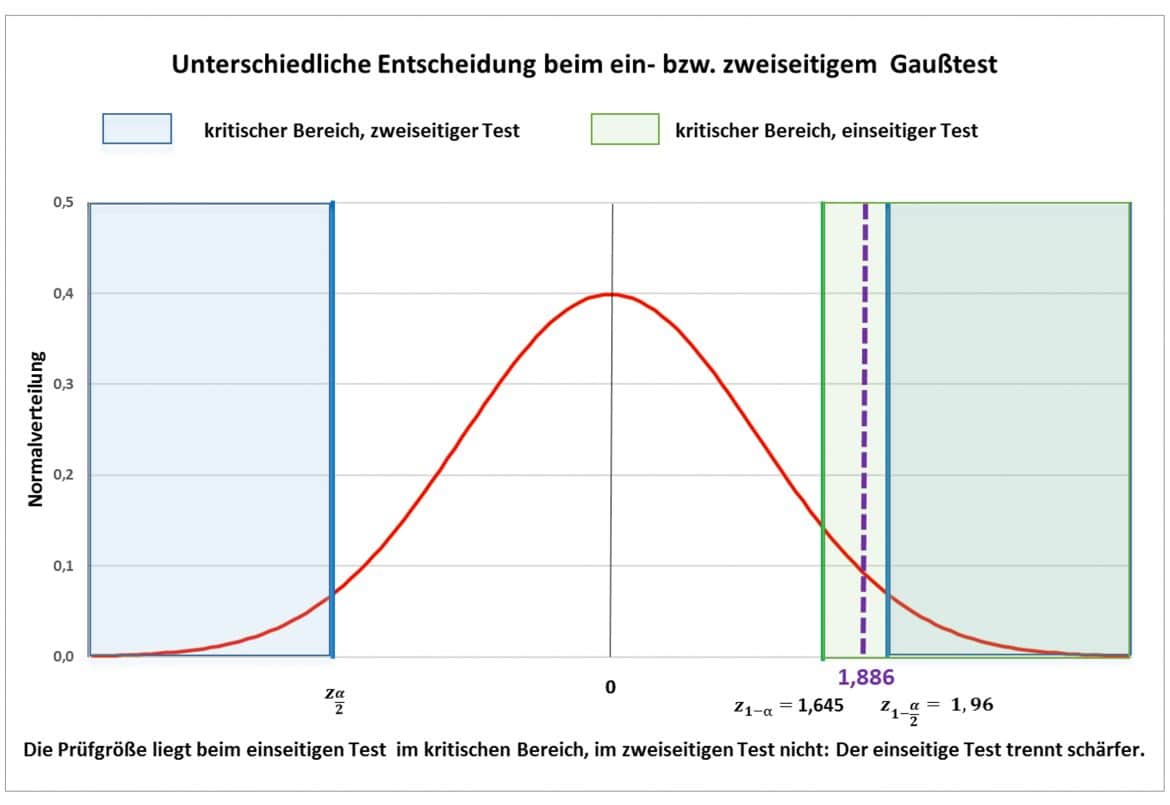gausstest-zweiseitig
Hättest Du dagegen einseitig zum gleichen Niveau von 5\% getestet, so hätte Dein Testergebnis mit

    \begin{equation*} 1,886 = z_{pr} > z_{kr} = z_{0,95} = 1,645\end{equation*}

zum Verwerfen der Nullhypothese geführt und Du hättest geschlossen, dass systematische Messfehler aufgetreten sind.

Daran kannst Du erkennen, dass einseitige Tests bei gleichem Signifikanzniveau eine schärfere Trennung bewirken als zweiseitige: falls Du daher eine Vermutung über die Richtung einer möglichen Ungleichheit hast, solltest Du immer den einseitigen Test wählen.