Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Chi-Quadrat Kontingenzanalyse
- 31. Mai 2017
- Posted by: Mika
Die Chi-Quadrat Kontingenzanalyse ist das geeignete Verfahren, wenn Du prüfen möchtest, ob zwei kategoriale Daten zusammenhängen. Bspw. könntest Du herausfinden wollen, ob sich Männer und Frauen hinsichtlich ihres Kaffeekonsums unterscheiden. Daraus würden z. B. die zweistufige Variable „Geschlecht“ (männlich/weiblich) und die dreistufige Variable „Kaffeekonsum“ (kein / wenig / viel) resultieren.
Erstellung einer Kontingenztabelle
Um zu testen, ob ein statistisch signifikanter Zusammenhang zwischen diesen beiden Variablen besteht, ist die Erstellung einer Kontingenztabelle erforderlich, in welche Du die Häufigkeiten Deiner Beobachtungen einträgst. Stell Dir vor, Du befragst 100 Männer und 100 Frauen hinsichtlich ihres Kaffeekonsums. Die aus diesen Daten entstehende Kontingenztabelle könnte folgendermaßen aussehen:
| Kaffeekonsum | ||||||
| kein | wenig | viel | Summe | Prozent | ||
| Geschlecht | männlich | 20 | 30 | 50 | 100 | 50 % |
| weiblich | 10 | 55 | 35 | 100 | 50 % | |
| Summe | 30 | 85 | 85 | 200 | ||
| Prozent | 15 % | 42.5 % | 42.5 % | 100 % | ||
Bei der ![]() Kontingenzanalyse vergleichst Du Deine beobachteten Häufigkeiten mit sogenannten erwarteten Häufigkeiten. Die erwarteten Häufigkeiten ergeben sich aus den Summen der Spalten und Zeilen der Kontingenztabelle, welche man als „Randverteilung“ bezeichnet.
Kontingenzanalyse vergleichst Du Deine beobachteten Häufigkeiten mit sogenannten erwarteten Häufigkeiten. Die erwarteten Häufigkeiten ergeben sich aus den Summen der Spalten und Zeilen der Kontingenztabelle, welche man als „Randverteilung“ bezeichnet.
In unserem Beispiel kannst Du die Randverteilung an der Zeile und Spalte mit der Beschriftung „Summe“ ablesen. Anhand der Randverteilung und der Stichprobengröße berechnest Du die Häufigkeiten, die zu erwarten wären, wenn Geschlecht und Kaffeekonsum unabhängig voneinander sind. Trägt man die erwarteten Häufigkeiten ebenfalls in eine Tabelle ein, ergibt sich für unser Beispiel folgendes Bild:
| Kaffeekonsum | ||||
| Geschlecht | kein | wenig | viel | |
| männlich | 15 | 42.5 | 42.5 | |
| weiblich | 15 | 42.5 | 42.5 | |
Formel des Chi-Quadrat Tests
Mit Hilfe des ![]() -Tests kannst Du nun überprüfen, ob sich die beobachteten und erwarteten Häufigkeiten signifikant voneinander unterscheiden. Dazu setzt Du in folgende Formel ein:
-Tests kannst Du nun überprüfen, ob sich die beobachteten und erwarteten Häufigkeiten signifikant voneinander unterscheiden. Dazu setzt Du in folgende Formel ein:
![]()
Für unser Beispiel ergibt sich dadurch:
![]()
Um zu überprüfen, ob sich die beobachteten Häufigkeiten signifikant von den erwarteten unterscheiden, musst Du den oben berechneten ![]() -Wert mit einem tabellarischen Wert vergleichen. Vorher benötigst Du allerdings noch die Freiheitsgrade Deines experimentellen Designs, welche Du folgendermaßen bestimmst:
-Wert mit einem tabellarischen Wert vergleichen. Vorher benötigst Du allerdings noch die Freiheitsgrade Deines experimentellen Designs, welche Du folgendermaßen bestimmst:
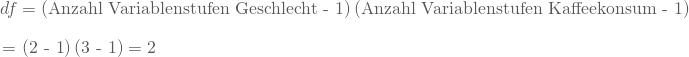
Der zu vergleichende ![]() -Wert beträgt bei einem Signifikanzniveau von 5 % und df = 2 beispielsweise 5.99. Der berechnete
-Wert beträgt bei einem Signifikanzniveau von 5 % und df = 2 beispielsweise 5.99. Der berechnete ![]() -Wert (
-Wert (![]() ) ist somit größer, als der Vergleichswert (
) ist somit größer, als der Vergleichswert (![]() ), was bedeutet, dass sich die Häufigkeiten signifikant unterscheiden und somit ein signifikanter Zusammenhang zwischen den Variablen Geschlecht und Kaffeekonsum besteht. Wäre der berechnete Wert nicht höher, wäre das Ergebnis auch nicht signifikant.
), was bedeutet, dass sich die Häufigkeiten signifikant unterscheiden und somit ein signifikanter Zusammenhang zwischen den Variablen Geschlecht und Kaffeekonsum besteht. Wäre der berechnete Wert nicht höher, wäre das Ergebnis auch nicht signifikant.
Wie stark ist der Zusammenhang?
Nun kannst Du noch prüfen, wie stark der von Dir gefundene Zusammenhang ist. Dazu werden meist Phi oder Cramers V berechnet. Phi variiert zwischen 0 und +1 und macht nur für 2×2 Tabellen Sinn, da der Koeffizient sonst kaum noch interpretierbar ist. Je weiter Phi vom Nullwert entfernt liegt, desto stärker ist der Effekt. Cramers V kann auch für größere Tabellen berechnet werden, wobei das Resultat bei 2×2 Tabellen immer ident mit jenem von Phi ist.
Um die beiden Größen zu berechnen, kannst Du folgende Formeln benutzen:
![]()
Bzw.
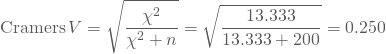
Da wir in unserem Beispiel keine 2×2 Tabelle aufgestellt haben, sondern eine 2×3, nehmen Phi und Cramers V nicht denselben Wert an (Phi = .258, Cramers V = .250). Die Werte unterscheiden sich nicht stark, aber trotzdem solltest Du darauf achten, das richtige Maß zu berechnen. Ab einem Wert von 0.30 wird meist von einem starken Effekt gesprochen, d. h. die von uns untersuchten Variablen weisen einen signifikanten mittelmäßig starken Zusammenhang auf.
Damit die ![]() Kontingenzanalyse valide Ergebnisse liefert, müssen folgende Voraussetzungen erfüllt sein:
Kontingenzanalyse valide Ergebnisse liefert, müssen folgende Voraussetzungen erfüllt sein:
- Bei den zu testenden Variablen muss es sich um kategoriale Daten handeln, d. h. sie weisen entweder nominales oder ordinales Skalenniveau auf.
- Dein Stichprobenumfang sollte mindestens 50 Personen (oder Testfälle, etc.) umfassen, da sich sonst zu wenig Fälle in jeder Zelle der Kontingenztabelle befinden könnten. Bei sehr kleinen Stichproben (N < 20) wird zur Korrektur der exakte Test nach Fisher angewandt, während die Korrektur nach Yates verwendet wird, wenn Deine Stichprobe zwischen 20 und 50 Personen beinhaltet.
- Die erwarteten Häufigkeiten, mit denen Deine Daten verglichen werden, müssen pro Zelle größer als 5 sein, sonst wird ebenfalls der exakte Test nach Fisher eingesetzt.
- Die Korrektur nach Yates würde wieder Anwendung finden, wenn die Freiheitsgrade (df) des
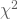 -Tests nicht größer als 1 sind.
-Tests nicht größer als 1 sind.
