Korrelationsanalyse

Korrelationsanalyse

  • 26. Januar 2017
  • Posted by: Mika
Keine Kommentare

Bei einer Korrelationsanalyse verwendest Du den Korrelationskoeffizienten nach Bravais Pearson als Maß für den linearen Zusammenhang zweier metrisch skalierter Variablen. Sein Quadrat, das Bestimmtheitsmaß, gibt an, welcher Anteil der Varianz durch ihren Zusammenhang erklärt werden kann. Dabei wird keine Aussage über den funktionalen Zusammenhang gegeben.

Möchtest Du anhand Deiner Stichprobe zweier Zufallsvariablen eine Schätzung für deren Korrelationskoeffizienten in den Grundgesamtheiten treffen, so kannst Du ihn aus der Stichprobe schätzen. Du kannst dann Hypothesen über Vermutungen zum Koeffizienten aufstellen und diese zu einem beliebigen Signifikanzniveau testen.

Voraussetzungen für dieses Vorgehen sind metrisch skaliertes Datenmaterial sowie Normalverteilung beider Zufallsvariablen in den Grundgesamtheiten. Mit dieser Methode kannst Du also lineare Zusammenhänge prüfen.

Wie sieht der Korrelationskoeffizient aus?

Der Korrelationskoeffizient \rho der Grundgesamtheit ist definiert als Quotient aus Kovarianz zwischen X und Y und dem Produkt der Standardabweichungen beider Variablen.

    \begin{equation*} \rho = \frac {Cov(X,Y)} {\sigma_X \cdot \sigma_Y} \end{equation*}

Er ist zudem dimensionslos und kann Werte zwischen -1 und +1 annehmen: Während -1 einen vollständigen negativen bzw. +1 einen vollständigen positiven linearen Zusammenhang bedeutet, teilt Dir ein Koeffizient von Null mit, dass die beiden Variablen unkorreliert miteinander sind und somit nicht zusammenhängen.

Stell Dir beispielsweise vor, Du bist im Marketing eines Elektronikunternehmens unter anderem für die Ausgestaltung der Preise zuständig. Ein neues Notebookmodell verkauft sich sehr schlecht und Du erwägst, eine Sonderverkaufsaktion mit reduziertem Preis zu initiieren. Das würde aber nur dann Sinn machen, wenn die Nachfrage in der Grundgesamtheit stark mit dem Preis zusammenhängt.

Da Preis und abgesetzte Stückzahlen metrisch skalierte Zufallsvariable sind, beschließt Du, eine Korrelationsanalyse durchzuführen, den Bravais-Pearson´schen Korrelationskoeffizienten aus der Stichprobe zu berechnen und anschließend zu testen, ob Preis und nachgefragte Menge tatsächlich korreliert sind.

Aufstellen von Hypothesen

    \begin{equation*} H_0: \rho =0 \quad gegen \quad H_1: \rho \ne 0\end{equation*}

Aus Deinen zehn größten belieferten Elektronikmärkten, die ihrerseits mit unterschiedlichen Preisen arbeiten, erhebst Du zuerst folgenden Verkaufszahlen des letzten Monats:

Markt 1 2 3 4 5 6 7 8 9 10 Durchschnitt
X: VK 459 399 425 499 465 489 419 444 497 449 454,5
Y: Stückzahl 11 17 16 5 13 4 14 12 4 12 10,8

Die Kombinationen von Preisen und nachgefragter Menge zeichnest Du dann in der Grafik als Punktwolke ein:

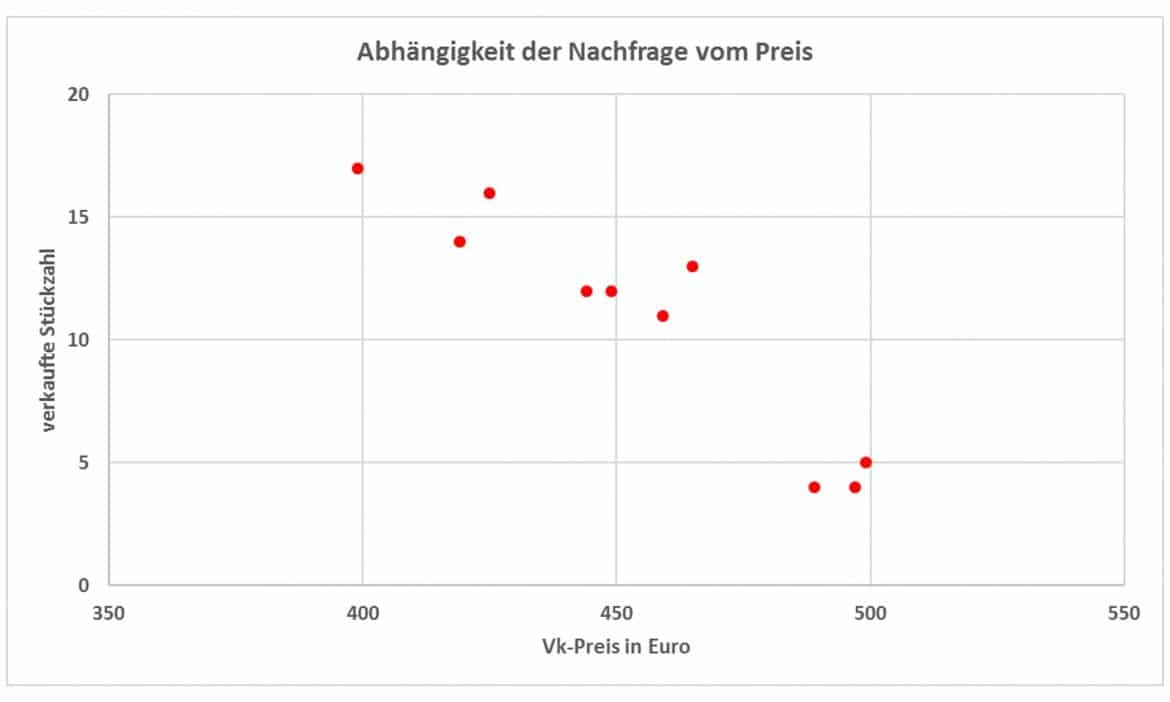
preis-und-stueckzahl

In der Grafik kannst Du deutlich einen negativen linearen Zusammenhang erkennen.

Als Schätzwert r für den Bravais-Pearson´schen Korrelationskoeffizienten \rho der Grundgesamtheit setzt Du anschließend erwartungstreue Schätzer für die Kovarianz und die Standardabweichungen ein:

    \begin{equation*} r= \frac {cov(x,y)} { s_x \cdot s_y} = \frac{\displaystyle \frac 1 {n-1} \sum_{i=1}^n {(x_i-\bar x) \cdot (y_i- \bar y)}}{\sqrt { \frac 1 {n-1} { \displaystyle \sum_{i=1}^n (x_i - \bar x)^2}}\cdot \sqrt { \frac 1 {n-1} { \displaystyle \sum_{i=1}^n (y_i - \bar y)^2}} } \end{equation*}

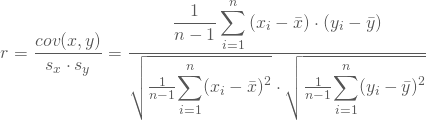
Für Dein Beispiel heißt das:

    \begin{equation*} r= \frac {-154,22} {{ \sqrt {23,289} \cdot \sqrt {1162,056} } }= -0,9375 \end{equation*}

In der Stichprobe besteht also wie vermutet ein hoher negativer Zusammenhang zwischen der verkauften Stückzahl und dem Preis.

Rückschluss auf die Grundgesamtheit

Danach möchtest Du testen, ob dieser negative Zusammenhang auch für die Grundgesamtheit angenommen werden kann, also ob für Dein Beispiel etwa ein negativer Zusammenhang von mehr als 75\% angenommen werden kann.

    \begin{equation*} H_0: \rho > -0,75 \quad gegen \quad H_1: \rho \le -0,75 \end{equation*}

Ein Korrelationskoeffizient \rho_0 zweier normalverteilter Zufallsvariablen ist nicht normalverteilt, lässt sich aber mittels der Fisher-Transformation in eine annähernd normalverteilte Zufallsvariable transformieren:

    \begin{equation*} f(\rho_0) = 0,5 \cdot ln \left(\frac { 1 + \rho_0} { 1-\rho_0}\right)\quad ist \quad N( 0,5 \cdot ln \left(\frac { 1 + \rho} { 1-\rho}\right); \frac 1 {\sqrt{n-3}})-verteilt \end{equation*}

Setzt Du schließlich für \rho_0 den aus Deiner Stichprobe ermittelten Schätzwert r = 0,9375 und für\rho den in Deinen Hypothesen zugrunde gelegten Wert von -0,75 ein, so ergibt sich durch Standardisierung von f Deine Testgröße:

    \begin{equation*} \frac {f(r) - f(\rho_0) -\rho_0/(n-2)} {\frac {1} {\sqrt{n-3}}} = \frac {f(-0,9375)-f(-0,75)-(0,75/8)} { \frac 1 {\sqrt 7}} = -1,704\end{equation*}

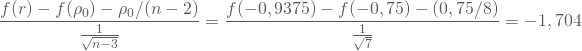
Diese kannst Du dann mit dem kritischen Wert der Standardnormalverteilung, etwa z_{kr} = z_{0,05}=-1,645 vergleichen und damit die Nullhypothese verwerfen: Mit einer Irrtumswahrscheinlichkeit von 5\% ist der Korrelationskoeffizient kleiner als -0,75.

Die Testentscheidung

Statistikprogrammsysteme geben in der Regel einen p-Wert aus. Dann kannst Du, anstatt die Teststatistik mit dem kritischen Wert zu vergleichen, alternativ den p-Wert dem von Dir vorgegebenen \alpha gegenüberstellen:

Du verwirfst die Nullhypothese, falls \alpha > p, anderenfalls gibt es keinen statistischen Grund, der gegen sie spricht.
Möchtest Du keine konkrete Hypothese über die Höhe der Korrelation sondern nur generell auf Signifikanz des Zusammenhangs testen,

    \begin{equation*} H_0: \rho = 0 \quad gegen \quad H_1: \rho \ne 0 \end{equation*}

so lässt sich Deine Prüfgröße vereinfachen zu

    \begin{equation*} \frac {r \cdot \sqrt {n-2}} { \sqrt {1-r^2}} \end{equation*}

Für große Stichproben (vorsichtig: n > 100) ist die Prüfgröße normalverteilt, für kleine Stichproben folgt sie einer t-Verteilung mit (n-2) Freiheitsgraden.

Um für Dein Beispiel zu testen, ob der ermittelte Korrelationskoeffizient signifikant von Null verschieden ist, setzt Du Deine Stichprobenwerte in die vereinfachte Prüfgröße ein und vergleichst sie mit dem kritischen t-Wert zum Niveau \alpha=5\% bei \nu=(n-2) Freiheitsgraden:

Mit

    \begin{equation*} t_{pr} = \frac {(-0,9375) \cdot \sqrt {8}} { \sqrt {1-(-0,9375)^2}} = 7,620 > 2,3060 = t_{(0,975;8)}} \end{equation*}

verwirfst Du die Nullhypothese und schließt auf einen signifikanten linearen Zusammenhang mit einer Irrtumswahrscheinlichkeit von 5\%.

Der Korrelationskoeffizient ist einfach auszurechnen und eine verbreitete Kenngröße, benötigt aber die beiden engen Voraussetzungen eines linearen Zusammenhangs und der Normalverteilung in der Grundgesamtheit.

Falls diese Voraussetzungen nicht gegeben sind, sind der Spearman´sche Rangkorrelationskoeffizient oder Kendalls W (Kendalls Konkordanzkoeffizient) eine brauchbare Alternative.