Chi-Quadrat-Anpassungstest

Chi-Quadrat-Anpassungstest

  • 18. November 2016
  • Posted by: Mika
Keine Kommentare

Mit dem Chi-Quadrat-Anpassungstest kannst Du testen, ob die Daten Deiner Stichprobe die Vermutung einer bestimmten Verteilung der Zufallsvariablen in der Grundgesamtheit zulassen. Du kannst ihn auf alle Skalenniveaus anwenden. Besonders für große Stichproben liefert er gute Ergebnisse.

Idee des Tests ist es, die beobachteten Häufigkeiten Deiner Stichprobe mit den theoretischen Häufigkeiten zu vergleichen, die zu erwarten wären, falls Deine Verteilungsvermutung zutrifft. Dabei müssen alle erwarteten Häufigkeiten größer als 5 sein.

Im Marketing eines Parfümerieunternehmens bist Du für eine neue Serie Deodorants zuständig, die in den Duftnoten Mandarine, Zitrone, Vanille, Zimt und Natur angeboten wird. Um Dein Marketinginstrumentarium optimal einzusetzen, möchtest Du untersuchen, ob sich alle fünf Duftrichtungen gleich gut verkaufen. Dazu erhebst Du eine Stichprobe von 1250 Testkäufern, die in der folgenden Tabelle aufgeführt sind:

lfd. Nr. Duftrichtung 
Deo Anzahl Verkäufe erwartete Häufigkeiten Differenz
1 Mandarine 175 250 -75
2 Zitrone 328 250 78
3 Vanille 192 250 -68
4 Zimt 257 250 7
5 Natur 298 250 48
1250 1250

Aufstellen von Hypothesen

Falls sich tatsächlich alle Duftnoten gleich gut verkaufen, könntest Du mit jeweils 250 verkauften Stück rechnen. Deine Hypothesen lauten:

H_0: die Zufallsvariable „Stückzahl nach Duftrichtung“ ist gleichverteilt.

H_1: die Zufallsvariable „Stückzahl nach Duftrichtung“ ist nicht gleichverteilt.

Falls die Nullhypothese gilt, sind Abweichungen zwischen den beobachteten und erwarteten Häufigkeiten nur auf Zufallseinflüsse zurückzuführen.

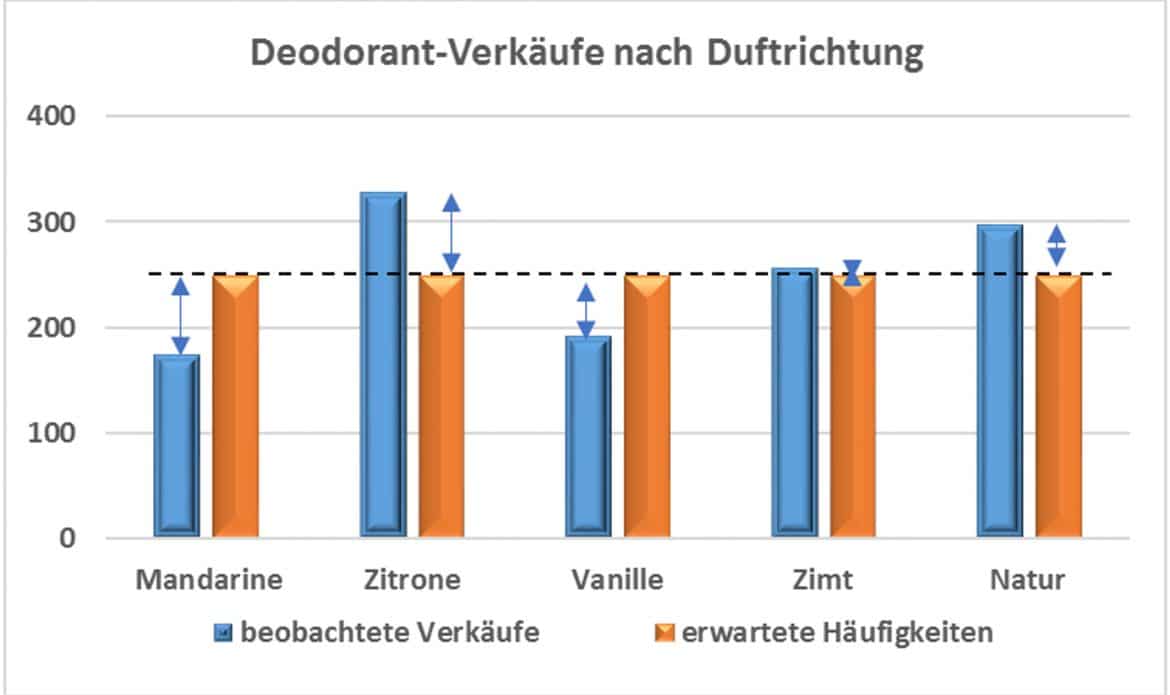
chiquadrat-anpassungstest

Je größer die Abweichungen sind, umso größer ist die Wahrscheinlichkeit, dass die Nullhypothese nicht gilt und die Duftrichtung systematischen Einfluss auf die Verkaufszahlen hat.

Teststatistik

Die Teststatistik (Chi-Quadrat-Koeffizient) des Chi-Quadrat-Tests addiert nun diese quadrierten Abweichungen, jeweils normiert mit den erwarteten Häufigkeiten.

    \begin{equation*} \chi^2 = \displaystyle \sum_{j=1} ^m \frac{(n_{j} - n \cdot p_{j })^2}{n \cdot p_{j}} = \frac{(-75)^2} {250} +\frac{78^2} {250} +\frac{(-68)^2} {250} +\frac{7^2} {250} +\frac{48^2} {250} = 69,704 \end{equation*}

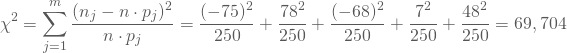
Als Summe von standardnormalverteilten Zufallsvariablen folgt sie einer Chi-Quadrat-Verteilung mit (m-1)=4 Freiheitsgraden. Daher vergleichst Du den Wert der Teststatistik mit dem der Chi-Quadrat-Verteilung beispielsweise zum Niveau \alpha = 5\% bei 4 Freiheitsgraden.

Mit

    \begin{equation*} 69,704 = \chi^2_{pr} > \chi^2_{kr} = 9,488 \end{equation*}

verwirfst Du die Nullhypothese der Gleichverteilung zum Niveau von 5\% und schließt, dass die Duftrichtung systematischen Einfluss auf die Verkaufszahlen hat.

Den Chi-Quadrat-Anpassungstest kannst Du für Zufallsvariablen aller Skalenniveaus verwenden.

Im Fall eines quantitativ stetigen Merkmals mit unendlich vielen möglichen Merkmalsausprägungen bildest Du zweckmäßigerweise Intervalle mit Ober-und Untergrenzen und verwendest die Klassenmitten. Je kleiner die Intervalle gewählt werden, desto genauer ist natürlich der Test. Laut Testvoraussetzung müssen sie aber so groß gewählt sein, dass alle erwarteten Häufigkeiten mindestens 5 betragen. Bei kleineren Stichproben musst Du daher oft die Intervalle in den Randbereichen vergrößern und erhältst so Unschärfebereiche.

Obwohl heute besonders für kleinere Stichproben bessere Test-Alternativen zur Verfügung stehen, ist der Chi-Quadrat-Anpassungstest immer noch recht verbreitet, was auch auf seine einfache rechentechnische Durchführung zurückzuführen ist, die auch von Hand erfolgen kann. Für große Stichproben ist er zuverlässig.