Kruskal-Wallis-Test / H-Test

Kruskal-Wallis-Test / H-Test

  • 21. März 2017
  • Posted by: Mika
Keine Kommentare

Der Kruskal-Wallis-Test oder H-Test ermöglicht es Dir, zwei oder mehr Stichproben mindestens ordinalskalierter Zufallsvariablen darauf zu untersuchen, ob sie hinsichtlich ihres Lageparameters aus der gleichen Verteilung stammen, ohne dass Du Verteilungsannahmen treffen musst. Das Vorgehen ist eine Verallgemeinerung des Mann-Whitney-Tests. Auf metrisch-skaliertes Datenmaterial kannst Du ihn anwenden, wenn die Voraussetzungen der parametrischen Tests nicht gegeben sind.

Wie bei der einfachen Varianzanalyse im Fall von metrisch-skaliertem Datenmaterial bedeutet ein signifikantes Testergebnis des Kruskal-Wallis-Tests, dass nicht alle Stichproben zu der gleichen Verteilung gehören. Der Test gibt dagegen keine Informationen darüber, wo die Unterschiede liegen.

Als zu erwartende Mittagstemperaturen für die nächsten vier Tage wurden vom Wetterdienst angegeben:

Frankfurt München Berlin
-1° 0° -2° -1° -3° -6° -5° -6° -2° -3° -4° -3°

Du möchtest testen, die ob die Temperaturen in den drei Städten unterschiedlich sind und formulierst Deine Hypothesen:

H_0: „Die Temperaturen weisen keine signifikanten Unterschiede auf“ gegen

H_1: „Die Temperaturen mindestens einer Stadt weichen von denen der anderen signifikant ab“.

Allgemein liegen Dir aus i=1 bis m Stichproben n_i Beobachtungen vor, die alle in eine gemeinsame Rangfolge gebracht werden. r_{ij} stellt den Rang der j-ten Beobachtung aus der i-ten Stichprobe dar.

Ordnen der Beobachtungen in eine gemeinsame Rangfolge

Für Dein Beispiel ordnest Du die Beobachungswerte aller Stichproben in eine gemeinsame Rangfolge, notierst, aus welcher Stichprobe sie jeweils stammen und ermittelst den Rangwert r_{ij} der j-ten Beobachtung aus der i-ten Stichprobe. Falls Bindungen auftreten, also mehrere Beobachtungen den gleichen Wert aufweisen, werden die Ränge gemittelt. Die kälteste Temperatur -6° beipielsweise wird zweimal erwartet. Daher werden hier die beiden ersten Ränge 1 und 2 zu einem gemeinsamen Rang 1,5 gemittelt. Es ergibt sich:

Stadt M M M B M B B F B F F F
Temperaturprognose -6° -6° -5° -4° -3° -3° -3° -2° -2° -1° -1° 0°
Rangwert r_{ij} 1,5 1,5 3 4 6 6 6 8,5 8,5 10,5 10,5 12

Berechnung des mittleren Rangwertes

Aus diesen Rangwerten r_{ij} berechnest Du dann den mittleren Rangwert aller Beobachtungen \bar r= 6,5, sowie die nach Städten getrennten mittleren Ränge zu \bar r_F = 2,5, \bar r_M = 6,625 und \bar r_B = 10,375. Schließlich bewertest Du Temperaturunterschiede als signifikant, falls die Unterschiede der durchschnittlichen Rangwerte der Städte zu groß sind.

Die Grafik zeigt die Temperaturen, dem Rang nach geordnet, sowie die mittleren Rangwerte.

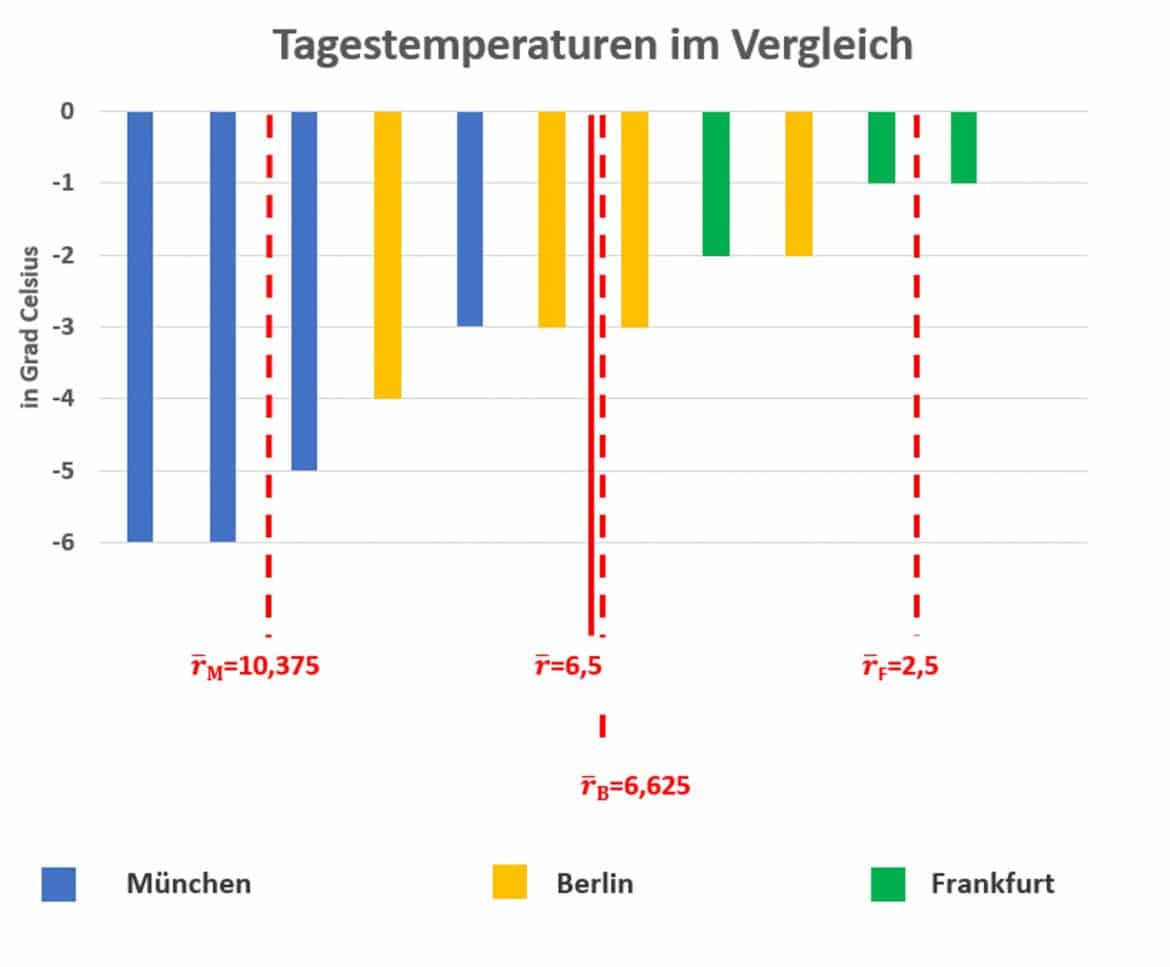
Kruskal-Wallis-Test / H-Test

Du betrachtest

  • zum einen die Summe der quadratischen Abweichungen des durchschnittlichen Rangs einer Stadt vom durchschnittlichen Rang insgesamt, jeweils gewichtet mit der Anzahl der Beobachtungen 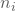n_i je Stadt.
  • Zum anderen betrachtest Du die Summe der quadratischen Abweichungen zwischen jedem beobachtetem Rangwert und dem insgesamt durchschnittlichen Rangwert über alle Städte und Beobachtungen.

Deine Teststatistik ergibt sich dann als Quotient dieser beiden Summen, multipliziert mit (N-1), wobei N die Gesamtanzahl der Beobachtungen ist:

    \begin{equation*} H = (N-1) \cdot \frac { \displaystyle \sum_{i=1}^m n_i \cdot (\bar r_i - \bar r)^2} {\displaystyle \sum_{i=1}^m \displaystyle \sum_{j=1}^{n_i} (r_{ij} - \bar r)^2 } \end{equation*}

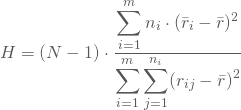
Für Dein Beispiel erhältst Du also:

    \begin{equation*} H = 11 \cdot \frac { (4 \cdot (2,5- 6,5)^2 + 4 \cdot (6,625 - 6,5)^2 + 4 \cdot (10,375-6,5)^2} {(1,5 - 6,5)^2 + (1,5 - 6,5)^2 + ... +(10,5-6,5)^2 + (12-6,5)^2 } = 9,788\end{equation*}

Die kritischen H-Werte liegen für kleine Stichproben tabelliert vor. Für größere Stichproben ist H approximativ \chi^2-verteilt, mit (m-1) Freiheitsgraden.

Bei Deinem Beispiel mit drei Stichproben zu je 4 Beobachtungen und einer Irrtumswahrscheinlichkeit von 5\% muss die Nullhypothese verworfen werden:

    \begin{equation*} H_{pr} = 9,788 > 5,692 = H_{kr} \end{equation*}

Du schließt, dass signifikante Temperaturunterschiede zwischen Frankfurt, München und Berlin bestehen.