Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Multiple Korrelationsanalyse
- 26. Januar 2017
- Posted by: Mika
Hast Du in Deiner Stichprobe die Werte von mehr als zwei metrischen Zufallsvariablen erhoben und vermutest einen linearen Zusammenhang zwischen einer Variablen Y und mehreren Variablen ![]() bis
bis ![]() , so ist die multiple Korrelationsanalyse die passende Methode. Wie bei der einfachen Korrelationsanalyse setzt Du Normalverteilung der Grundgesamtheiten voraus.
, so ist die multiple Korrelationsanalyse die passende Methode. Wie bei der einfachen Korrelationsanalyse setzt Du Normalverteilung der Grundgesamtheiten voraus.
Definition des multiplen Korrelationskoeffizienten
Der multiple Korrelationskoeffizient ist definiert als Wurzel aus dem multiplen Bestimmtheitsmaß, das den Anteil der durch die Variablen erklärte Varianz an der Gesamtvarianz ergibt. Er kann zudem nur positive Werte zwischen Null und eins annehmen.
Du kannst den Wert des multiplen Bestimmtheitsmaßes als Funktion der einfachen Korrelationskoeffizienten von allen beteiligten Variablen ermitteln. Das heißt Du gehst von der Summe der quadrierten Korrelationskoeffizienten ![]() zwischen Y und allen
zwischen Y und allen ![]() aus. Dann subtrahierst Du davon die wechselseitigen Beeinflussungen
aus. Dann subtrahierst Du davon die wechselseitigen Beeinflussungen ![]() zwischen allen Paaren von
zwischen allen Paaren von ![]() und
und ![]() . Anschließend normierst Du den Ausdruck durch den nicht durch Wechselwirkung erklärten Zusammenhang.
. Anschließend normierst Du den Ausdruck durch den nicht durch Wechselwirkung erklärten Zusammenhang.
Im Falle von drei zusammenhängenden Variablen Y, ![]() und
und ![]() hast Du den multiplen Koeffizienten gegeben als:
hast Du den multiplen Koeffizienten gegeben als:
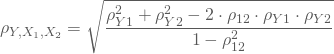
Für dessen Schätzwert ![]() setzt Du die Schätzwerte
setzt Du die Schätzwerte ![]() der einfachen Korrelationskoeffizienten ein.
der einfachen Korrelationskoeffizienten ein.
Beispiel für eine multiple Korrelationsanalyse
Stell Dir vor, Du sollst ein ökonomisches Modell testen, nach dem die monatlichen Haushaltsausgaben Y zum einen mit dem verfügbarem Einkommen ![]() und zum anderen mit dem Vermögen
und zum anderen mit dem Vermögen ![]() zusammenhängen. Dazu hast Du folgendes Datenmaterial erhoben:
zusammenhängen. Dazu hast Du folgendes Datenmaterial erhoben:
| Haushaltsnummer | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| in € | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Ausgaben | Y | 650 | 1.200 | 4.500 | 1.800 | 3.300 | 4.800 | 6.200 | 3.200 | 5.000 | 3.300 |
| verfügbares Einkommen | 1.800 | 1.600 | 5.500 | 1.600 | 2.700 | 7.200 | 7.200 | 2.800 | 8.000 | 3.300 | |
| Vermögen | 0 | 2.000 | 85 | 0 | 12.000 | 50.000 | 0 | 18.000 | 70.000 | 10.000 | |
Daraus errechnest Du als erstes die einfachen Korrelationskoeffizienten der Stichprobe zwischen allen Kombinationen von je zwei Variablen:
- Die Korrelation zwischen Ausgaben und verfügbarem Einkommen beträgt
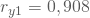 ,
, - Korrelation zwischen Ausgaben und Vermögen :
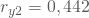
- Korrelation zwischen verfügbarem Einkommen und Vermögen:
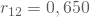
Setzt Du diese Werte in die Formel für den Schätzwert des multiplen Regressionskoeffizienten ein,
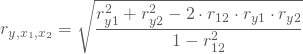
so erhältst Du
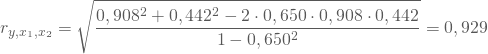
Der multiple Korrelationskoeffizient zwischen Ausgaben, Einkommen und Vermögen in Deiner Stichprobe beträgt also 0,929 und spricht für einen hohen Zusammenhang zwischen den drei Variablen.
Ist der Zusammenhang statistisch signifikant?
Es bleibt Dir aber noch zu prüfen, ob dieser Zusammenhang statistisch signifikant ist, ob Du also das Ergebnis der Stichprobe verallgemeinern kannst.
Dazu stellst Du als Deine Hypothesen auf:
![]() : es besteht kein multipler Zusammenhang zwischen Y,
: es besteht kein multipler Zusammenhang zwischen Y, ![]() und
und ![]() .
.
![]() : es besteht ein multipler Zusammenhang zwischen Y,
: es besteht ein multipler Zusammenhang zwischen Y, ![]() und
und ![]() .
.
Als Testgröße berechnest Du dann den Quotienten
![]()
Dabei stehlt n für die Anzahl der Beobachtungen und k für die Anzahl der Variablen ![]() . Die Testgröße ist F-verteilt, mit (k;n-k-1) Freiheitsgraden.
. Die Testgröße ist F-verteilt, mit (k;n-k-1) Freiheitsgraden.
Für Deine Untersuchung gilt: Mit
![]()
verwirfst Du die Nullhypothese und schließt, dass ein signifikanter multipler Zusammenhang besteht.
Falls Du die Nullhypothese aufgrund der Stichprobenergebnisse nicht verwirfst, bedeutet das nicht, dass kein Zusammenhang zwischen beteiligten Variablen besteht. Es heißt vielmehr, dass nicht alle betrachteten Variablen miteinander zusammenhängen. Du solltest dann Deine Analyse für eine andere Variablengruppierung wiederholen.
Der multiple Korrelationskoeffizient ist also umso interessanter, je weniger die ![]() untereinander korrelieren, gleichzeitig jedoch einzeln mit Y möglichst stark zusammenhängen.
untereinander korrelieren, gleichzeitig jedoch einzeln mit Y möglichst stark zusammenhängen.
