Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Shapiro-Wilk-Test
- 18. November 2016
- Posted by: Mika
Mit dem Shapiro-Wilk-Test hast Du für metrische Daten einen starken Test auf Normalverteilung gegeben, der für Stichprobengrößen ab 3 Beobachtungen eingesetzt werden kann. Damit kannst Du ihn auch bei sehr kleinen Stichproben verwenden und prüfen, ob die Daten der Normalverteilungsannahme widersprechen, die bei parametrischen Tests oft gefordert wird.
Bei einer Untersuchung von n=12 Patienten mit einer seltenen Herzkrankheit hast Du beispielsweise unter anderem den diastolischen Blutdruck erhoben. Da Du diesen mit Hilfe von parametrischen Testverfahren weiter untersuchen möchtest, möchtest Du zuerst auf Normalverteilung testen und entscheidest Dich daher für den Shapiro-Wilk-Test.
| Lfd. Nummer i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diastolischer
Blutdruck |
64 | 68 | 70 | 70 | 80 | 80 | 82 | 84 | 84 | 86 | 92 | 99 |
Aufstellen von Hypothesen
Deine Hypothesen lauten entsprechend:
![]() : die Zufallsvariable „Diastolischer Blutdruck“ folgt einer Normalverteilung
: die Zufallsvariable „Diastolischer Blutdruck“ folgt einer Normalverteilung
![]() : die Zufallsvariable „Diastolischer Blutdruck“ folgt keiner Normalverteilung
: die Zufallsvariable „Diastolischer Blutdruck“ folgt keiner Normalverteilung
Als Teststatistik bildest Du den Quotienten aus zwei Schätzungen für die Varianz:
![]()
- der unter Normalverteilung erwarteten Varianz der Stichprobe
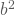
- und der nicht korrigierten Stichprobenvarianz
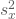
![]() kannst Du damit als Korrelationskoeffizienten interpretieren, der Werte zwischen Null und eins annehmen kann. Falls die Nullhypothese gilt, müssten beide Schätzungen also ähnlich ausfallen und der Wert der Teststatistik in der Nähe von 1 liegen. Je kleiner
kannst Du damit als Korrelationskoeffizienten interpretieren, der Werte zwischen Null und eins annehmen kann. Falls die Nullhypothese gilt, müssten beide Schätzungen also ähnlich ausfallen und der Wert der Teststatistik in der Nähe von 1 liegen. Je kleiner ![]() zudem wird, umso wahrscheinlicher ist es also, dass die Nullhypothese verworfen werden muss. Die kritischen Werte liegen übrigens in Abhängigkeit vom Stichprobenumfang und des Signifikanzniveaus tabelliert vor und die Nullhypothese wird verworfen, falls
zudem wird, umso wahrscheinlicher ist es also, dass die Nullhypothese verworfen werden muss. Die kritischen Werte liegen übrigens in Abhängigkeit vom Stichprobenumfang und des Signifikanzniveaus tabelliert vor und die Nullhypothese wird verworfen, falls
![]()
Die Testentscheidung
Für die unter der Normalverteilung zu erwartete Varianz ![]() sortiert der Shapiro-Wilk-Test die Stichprobenwerte in aufsteigender Reihe und berechnet paarweise die Differenzen zwischen dem größten und kleinsten, dem zweitgrößten und zweitkleinsten Wert usw., bis im Fall einer geraden Anzahl von Stichprobenwerten alle Werte berücksichtigt sind oder bei ungeraden Anzahlen der mittlere Wert übrigbleibt. Diese Differenzen werden dann mit vom Testverfahren vorgegebenen Koeffizienten multipliziert, über alle Paare addiert und die Summe quadriert. Für Dein Beispiel berechnest Du folglich für den Nenner der Teststatistik
sortiert der Shapiro-Wilk-Test die Stichprobenwerte in aufsteigender Reihe und berechnet paarweise die Differenzen zwischen dem größten und kleinsten, dem zweitgrößten und zweitkleinsten Wert usw., bis im Fall einer geraden Anzahl von Stichprobenwerten alle Werte berücksichtigt sind oder bei ungeraden Anzahlen der mittlere Wert übrigbleibt. Diese Differenzen werden dann mit vom Testverfahren vorgegebenen Koeffizienten multipliziert, über alle Paare addiert und die Summe quadriert. Für Dein Beispiel berechnest Du folglich für den Nenner der Teststatistik
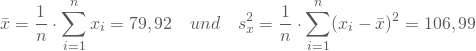
sowie für den Zähler die Summe der paarweisen Differenzen von außen nach innen, jeweils multipliziert mit testspezifischen Koeffizienten:
![Rendered by QuickLaTeX.com \begin{align*} b^2 = [&0,5475 \cdot (99-64) + 0,3325 \cdot (92-68) + 0,2347 \cdot (86-70) + \\ &0,1586 \cdot (84-70) +0,0922 \cdot (84-80) + 0,0303 \cdot (82-80)]^2=1125,43 \end{align*}](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-b0fa07c0c7bb60a52b6e25335b743f83_l3.png)
Deine Testentscheidung lautet demnach
![]()
und Du schließt, dass Du die Nullhypothese einer Normalverteilung aufgrund Deiner Daten nicht verwerfen musst.
