Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Wald Wolfowitz Runs Test
- 21. März 2017
- Posted by: Mika
Hast Du eine Folge von Realisationen einer dichotomen Zufallsvariablen gegeben, die also nur zwei Ausprägungen annehmen kann, so prüfst Du mit dem Wald Wolfowitz Runs Test, ob diese Folge zufällig ist. Dazu untersuchst Du, wie häufig es zu einem Wechsel von aufeinanderfolgenden gleichartigen Realisationen der Zufallsvariablen kommt. Diese nennt man dann „Lauf“ oder „Run“ der Folge, die Anzahl der Runs ist mit Deiner Zufallsvariablen R gegeben.
Als Marktforscher möchtest Du beispielsweise das Konsumentenverhalten bei der Nutzung des Telefons untersuchen. Dazu notierst Du bei den Anrufen, die an einem Tag eingehen, ob sie vom Festnetz (F) oder vom Mobiltelefon (M) aus getätigt werden. Du erhältst mit
| M M M M | F F F | M M M | F F | M M M M M M | F F F F | M M |
| 1. Run | 2. Run | … | … | … | … | 7. Run |
eine beobachtete Anzahl von r=7 Runs, Folgen von aufeinanderfolgenden gleichen Realisationen.
Im Fall einer geraden Anzahl von Runs ist die Anzahl der Runs beider Beobachtungsausprägungen gleich, r = 2q. Im Fall einer ungeraden Anzahl ist dagegen eine der beiden Anzahlen um eins höher als die andere und es gilt: r = 2q+1. Hier wurden demnach q=3 Runs von „F“ und q+1=4 Runs von „M“ beobachtet.
Wie lautet die Nullhypothese?
Deine Nullhypothese lautet, die Realisationen seien unabhängig voneinander gezogen und die Anzahl der Läufe zufällig zustande gekommen. Um diese Hypothese zu überprüfen, untersuchst Du mithilfe der Kombinatorik die Wahrscheinlichkeiten für verschiedene Anzahlen R von Läufen als Anzahl der günstigen, dividiert durch Anzahl der möglichen Anordnungen.
Bei n=24 Beobachtungen und k=15-maligem Auftreten von „M“ gibt es insgesamt ![]() mögliche Anordnungen der Beobachtungen.
mögliche Anordnungen der Beobachtungen.
Bezüglich der günstigen Läufe muss zwischen geraden und ungeraden Anzahlen unterschieden werden.
Gerade Anzahl von Läufen
Es gibt ebensoviele Läufe von „M“ wie von „F“, es gilt: r=2q und die erste Beobachtung des ersten Runs ist „M“. Die Anzahl der Möglichkeiten, bei n Beobachtungen insgesamt, (k-1) verbliebene Beobachtungen von „M“ in (r-1) Läufe anzuordnen, beträgt ![]() .
.
Da es für die Anordnung der Läufe egal ist, ob der erste Lauf mit „M“ oder „F“ beginnt, multiplizierst Du diesen Term für die Anzahl der günstigen Fälle im geraden Fall mit 2 und die Wahrscheinlichkeit ergibt sich zu:
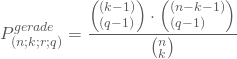
Ungerade Anzahl von Läufen
Bei ungeraden Anzahlen von Läufen muss die Anordnung mit der Merkmalsausprägung beginnen, deren Laufzahl höher ist. Möglich ist dies für beide. Die Wahrscheinlichkeit, für gegebene Anzahlen von n und k entweder genau (q+1) Läufe von „M“ und q Läufe von „F“ zu beobachten, oder genau q Läufe von „M“ und (q+1) Läufe von „F“ anzuordnen, beträgt dann
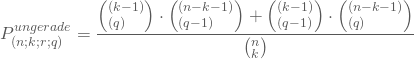
Mit diesen Formeln lässt sich die Verteilung von R als Wahrscheinlichkeit berechnen, für gegebene n und k eine Anzahl von r Läufen oder weniger zu erhalten. Für Dein Beispiel mit n=24 und k=15 ergibt sich:
| r | |
|---|---|
| 3 | 0,0000 |
| 4 | 0,0001 |
| 5 | 0,0010 |
| 6 | 0,0029 |
| 7 | 0,0146 |
| 8 | 0,0302 |
| 9 | 0,0926 |
| 10 | 0,1461 |
| 11 | 0,2962 |
| 12 | 0,3819 |
| 13 | 0,5534 |
| … | … |
Wann wird die Nullhypothese verworfen?
Die Wahrscheinlichkeit unter der Nullhypothese, bei n=24 Anrufen und k=15 Mobilfunknummern nur r=7 oder weniger Runs zu beobachten, ist also kleiner als ![]() . Du verwirfst daher die Nullhypothese, die Runs seien zufällig zustande gekommen.
. Du verwirfst daher die Nullhypothese, die Runs seien zufällig zustande gekommen.
Allgemein verwirfst Du die Nullhypothese zu einer vorgegebenen Irrtumswahrscheinlichkeit ![]() , falls r zu groß oder zu klein ist. Im zweiseitigen Fall lautet Deine Testentscheidung „Verwerfen der Nullhypothese“, falls
, falls r zu groß oder zu klein ist. Im zweiseitigen Fall lautet Deine Testentscheidung „Verwerfen der Nullhypothese“, falls
![]()
Ab k>20 und (n-k) > 20 folgt R asymptotisch einer Standardnormalverteilung mit den Parametern
![]()
Dann kannst Du die Anzahl der Runs standardisieren und mit dem kritischen Wert der Standardnormalverteilung vergleichen.
Für die Parameter Deines Beispiels, die die Approximationsbedingung streng genommen nicht erfüllen, ergäbe sich:
![]()
und Du erhältst:
![]()
Auch bei der Approximation durch die Standardnormalverteilung, die hier aufgrund der Anzahl strenggenommen nicht erlaubt war, verwirfst Du die zweiseitige wie die einseitige Nullhypothese zum Niveau von ![]() .
.
