Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Wilcoxon-Vorzeichen-Rang-Test
- 21. März 2017
- Posted by: Mika
Der Wilcoxon-Vorzeichen-Rang-Test ermöglicht es Dir, zwei abhängige Stichproben von mindestens ordinalskalierten Zufallsvariablen X und Y auf Gleichheit der zentralen Tendenz zu untersuchen. Er stellt damit für verbundene Stichproben eine Alternative zum t-Test dar, wenn dessen Voraussetzungen eines metrischen Skalenniveaus oder der Normalverteilung der Grundgesamtheit nicht erfüllt sind.
Du testet die Nullhypothese, paarweise Unterschiede zwischen den Beobachtungen beider Stichproben seien symmetrisch um Null verteilt, gegen die ein- oder zweiseitige Alternativhypothese.
Stell Dir vor, Du bist Arzt und erhebst unter anderem den Cholesterinwert LDL Deiner Patienten (X). Eine Gruppe von 10 Patienten nimmt an einem sechswöchigen Sportkurs teil und Du erhebst ihren LDL-Wert danach erneut (Y), um zu testen, ob die geänderte Lebensweise zu einer signifikanten Senkung des Wertes geführt hat.
Die ersten drei Spalten der Tabelle enthalten Deine erhobenen Daten. Spalte 4 enthält zudem die Wertänderung, Spalte 5 das Vorzeichen der Änderung, multipliziert mit 1, und Spalte 6 den absoluten Wert der Änderung.
| lfd. Nr. i |
Messung 1 |
Messung 2 |
Differenz |
Vorzeichen der Differenz |
Absolutwert der Differenz |
|---|---|---|---|---|---|
| 1 | 125 | 110 | -15 | -1 | 15 |
| 2 | 115 | 122 | 7 | 1 | 7 |
| 3 | 130 | 125 | -5 | -1 | 5 |
| 4 | 140 | 120 | -20 | -1 | 20 |
| 5 | 140 | 140 | 0 | 0 | 0 |
| 6 | 115 | 114 | -1 | -1 | 1 |
| 7 | 140 | 123 | -17 | -1 | 17 |
| 8 | 125 | 137 | 12 | 1 | 12 |
| 9 | 140 | 135 | -5 | 1 | 5 |
| 10 | 135 | 125 | -10 | -1 | 10 |
Unterschied zum t-Test
Während Du beim t-Test im Fall von metrisch-skaliertem Datenmaterial die (standardisierten) Differenzen betrachtest, die sich unter der Nullhypothese zu Null addieren müssten, betrachtest Du hier, ob Änderungen in eine der beiden Richtungen systematisch größer als in die andere sind. Du untersuchst dazu die Rangwerte der absoluten Differenzen zwischen Beobachtungen von X und Y. Falls kein signifikanter Unterschied zwischen X und Y besteht, müsste die Summe der Rangwerte, die sich auf vergrößerte Werte beziehen ähnlich hoch sein wie die Summe der Rangwerte, die zu reduzierten Werten gehören.
Vorgehen beim Wilcoxon-Vorzeichen-Rang-Test
Du sortierst Deine Daten zuerst aufsteigend nach der absoluten Höhe der Änderungen, wie die zweite Tabelle zeigt. Alle Beobachtungen, die keine Änderung aufweisen, werden dann gestrichen, und die Anzahl der relevanten Datensätze reduziert sich auf ![]() .
.
Die verbleibenden Werte werden mit aufsteigenden Rangwerten versehen. Falls Bindungen auftreten, also der gleiche Wert mehrmals auftritt, werden die Rangwerte gemittelt. Die absolute Differenz von 5 tritt zum Beispiel bei den Probanden 6 und 3 auf. Anstelle der Ränge zwei und drei also erhalten also beide den Rangwert 2,5. Die letzte Spalte der Tabelle enthält den Rangwert des jeweiligen Probanden, multipliziert mit dem Vorzeichen seiner Änderung.
| i | Rangwert
|
||||||
|---|---|---|---|---|---|---|---|
| 5 | 140 | 140 | 0 | 0 | (gestrichen) | ||
| 6 | 115 | 114 | -1 | -1 | 1 | 1 | -1 |
| 3 | 130 | 125 | -5 | -1 | 5 | 2,5 | -2,5 |
| 9 | 140 | 135 | -5 | -1 | 5 | 2,5 | -2,5 |
| 2 | 115 | 122 | 7 | 1 | 7 | 4 | 4 |
| 10 | 135 | 125 | -10 | -1 | 10 | 5 | -5 |
| 8 | 125 | 137 | 12 | 1 | 12 | 6 | 6 |
| 1 | 125 | 110 | -15 | -1 | 15 | 7 | -7 |
| 7 | 140 | 123 | -17 | -1 | 17 | 8 | -8 |
| 4 | 140 | 120 | -20 | -1 | 20 | 9 | -9 |
Berechnen der Teststatistik
Addierst Du jetzt alle positiven Rangwerte zu ![]() und alle negativen betragsmäßig zu
und alle negativen betragsmäßig zu ![]() , so ergibt sich Deine Teststatistik zu
, so ergibt sich Deine Teststatistik zu
![]()
Die kritischen Werte liegen bis ![]() tabelliert vor und für Dein Beispiel ergibt sich: Mit
tabelliert vor und für Dein Beispiel ergibt sich: Mit
![]()
kannst Du Deine Nullhypothese nicht verwerfen. Die Stichprobe hat also keine signifikante Reduzierung des Cholesterinwertes durch den Sportkurs ergeben.
Für größere n arbeitest Du mit einer modifizierten Testgröße ![]() , die sich als Summe der mit dem Vorzeichen multiplizierten und über alle i summierten Rangwerte ergibt:
, die sich als Summe der mit dem Vorzeichen multiplizierten und über alle i summierten Rangwerte ergibt:
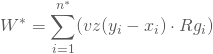
Falls die Nullhypothese gilt, folgt ![]() einer spezifischen Verteilung mit dem Mittelwert 0 und der Varianz
einer spezifischen Verteilung mit dem Mittelwert 0 und der Varianz ![]() ; für große
; für große ![]() kannst Du sie durch die Normalverteilung approximieren.
kannst Du sie durch die Normalverteilung approximieren.
Du verwirfst dann die Nullhypothese, falls das standardisierte ![]() größer als der kritische Wert der Standardnormalverteilung zur gewählten Irrtumswahrscheinlichkeit ist;
größer als der kritische Wert der Standardnormalverteilung zur gewählten Irrtumswahrscheinlichkeit ist; ![]() wird also verworfen, falls:
wird also verworfen, falls:
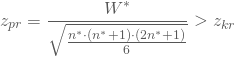
Viele Statistikprogrammsysteme geben Dir Testergebnis einen p-Wert aus. Damit entscheidest Du auf ein Verwerfen der Nullhypothese, falls der p-Wert kleiner als die von Dir gewählte Irrtumswahrscheinlichkeit ist.
