Log-Rank-Test

Log-Rank-Test

  • 21. März 2017
  • Posted by: Mika
Keine Kommentare

Mit dem Log-Rank-Test kannst Du die „Überlebenswahrscheinlichkeiten“ oder „Verbleibedauern“ der Elemente zweier Stichproben miteinander vergleichen. Er wird in der medizinischen Statistik oft eingesetzt, um die zeitliche Wirkung eines Medikamentes an einer Stichprobe im Vergleich mit einer Kontrollgruppe zu testen. Beispielsweise könnte man überprüfen, ob der Ausbruch einer bestimmten Krankheit durch den Einsatz eines Medikamentes verzögert wird. Du kannst ihn analog auf alle Situationen anwenden, in denen die Zeit bis zum Eintreffen eines bestimmten Ereignisses verglichen werden soll.

Allgemein testest Du die Nullhypothese, es bestehe kein signifikanter Unterschied zwischen Test- und Kontrollgruppe.

Stell Dir vor, eine Personalagentur bietet ein Angebot für Hochschulabsolventen an und verspricht, dass ihre Klienten schneller einen Arbeitsvertrag unterschreiben als diejenigen, die nicht mit der Agentur zusammenarbeiten. Als unabhängiger Tester möchtest Du diese Aussage überprüfen. Dazu beobachtest Du eine Testgruppe von anfänglich n_{11}= 25 Jungakademikern, die die Dienstleistung der Agentur nutzen und vergleichst sie mit einer Kontrollgruppe vom Anfangsumfang n_{21}=30.

Wie sehen die Daten aus?

In jeder Woche i dokumentierst Du die folgenden Informationen.

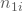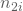  • Wie viele Personen sind aus beiden Gruppen 1 und 2 zu Beginn der Woche ohne Arbeitsvertrag. Damit erhältst Du die Anzahlen n_{1i} und n_{2i}, sowie die Gesamtanzahl 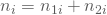n_i= n_{1i} + n_{2i} zum Zeitpunkt i.
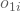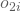  • Die Anzahl an geschlossenen Arbeitsverträgen o_{1i} und o_{2i} in der Woche i sowie deren Summe o_i= o_{1i} + o_{2i}.

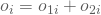Du erhältst also folgende Daten:

Woche mit Agentur ohne Agentur beide Gruppen gemeinsam
noch zu vermittelnde
 Personen Vertrags-
abschlüsse		 noch zu vermittelnde
 Personen Vertrags-
abschlüsse		 noch zu vermittelnde
 Personen Vertrags-
abschlüsse
n_{1i} o_{1i} n_{2i} o_{2i} n_{i} o_{i}
1 25 4 30 3 55 7
2 21 3 27 1 48 4
3 18 3 26 6 44 9
4 15 3 20 2 35 5
5 12 5 18 2 30 7
6 7 4 16 5 23 9

Das Diagramm legt die Vermutung nahe, dass die Mitglieder Deiner Testgruppe (blau) schneller zum Vertragsabschluss kommen als die der (orangen) Kontrollgruppe , die ohne Agentur arbeiten:

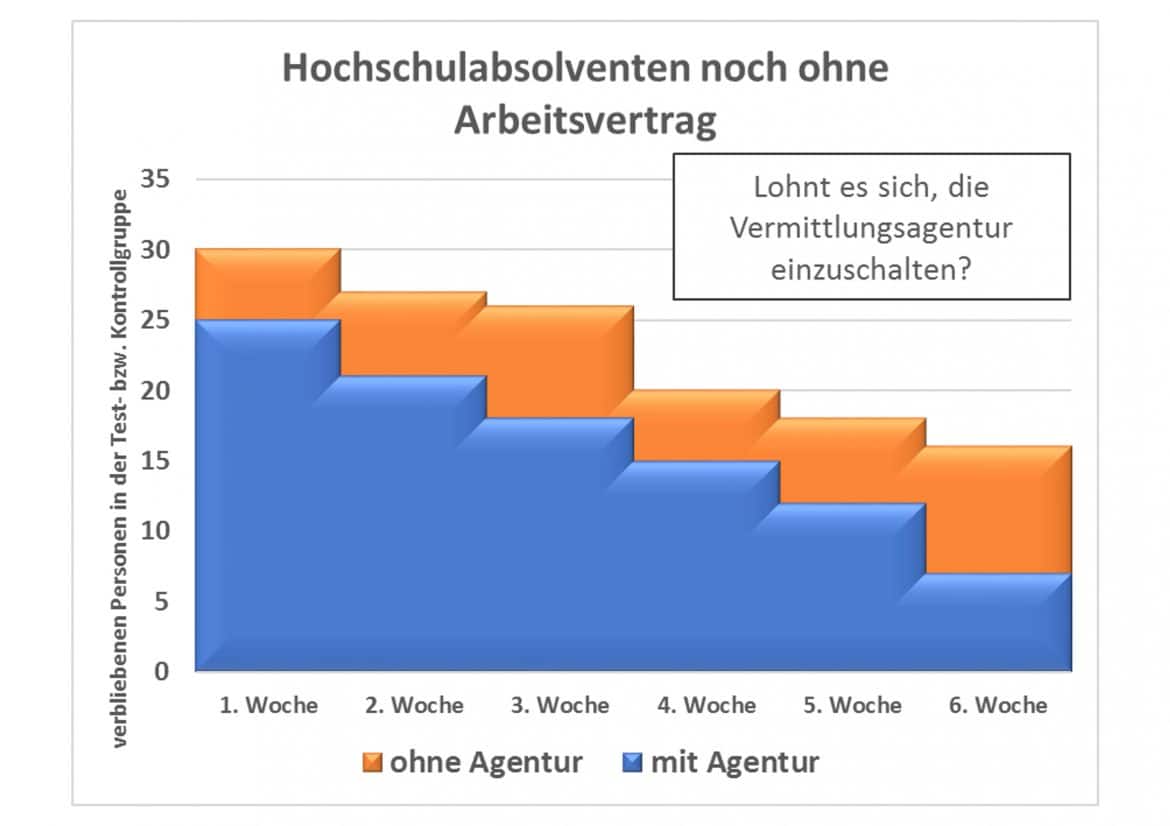Log-Rank-TestIst dieser Unterschied signifikant?

Falls keine signifikanten Unterschiede zwischen den beiden Gruppen bestehen, könntest Du als Schätzwert für die Wahrscheinlichkeit eines Vertragsabschlusses in der i-ten Woche für beide Gruppen die relative Häufigkeit der Gesamtgruppe verwenden.

    \begin{equation*} \hat p_i = \frac {o_i} { n_i }= \frac {o_{1i} + o_{2i} } {n_{1i} + n_{2i} } \end{equation*}

Erwartungswert und Varianz der in der i-ten Woche unter dieser Hypothese zu erwartenden Anzahl von abgeschlossenen Verträgen in der Testgruppe ergäbe sich dann zu:

    \begin{equation*} E(O_{1i}) = \frac {o_i} {n_i} \cdot n_{1i} \quad und \quad Var(O_{1i}) = \frac { o_i \cdot \frac {n_{1i}} {n_i} \cdot (n_i - o_i)\cdot(1-\frac {n_{1i}} {n_i}) } {n_i - 1 } \end{equation*}

Du berechnest nun pro Woche die Differenz zwischen den in der Testgruppe tatsächlich beobachteten und den unter der Nullhypothese zu erwartenden Vertragsabschlüssen. Diese Werte standardisierst Du anschließend, indem Du sie durch die erwartete Standardabweichung \sqrt { \displaystyle \sum_{i=1}^6 Var (O_{i}}) dividierst.

i o_{1i} o_i n_i \frac {o_i} {n_i} E(O_i) Var(O_i) o_i - E(O_i) \frac {( o_i - E(O_i) }{{\sqrt { \displaystyle \sum_{i=1}^6 Var (O_{i}})}}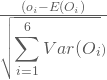
1 4 7 55 0,127 3,182 1,543 0,818 0,292
2 3 4 48 0,083 1,75 0,922 1,25 0,446
3 3 9 44 0,205 3,682 1,771 -0,682 -0,243
4 3 5 35 0,143 2,143 1,08 0,857 0,306
5 5 7 30 0,233 2,8 1,332 2,2 0,785
6 4 9 23 0,391 2,739 1,213 1,261 0,450
Summe 7,861 2,035

Wie sieht die Teststatistik aus?

Deine Teststatistik ergibt sich dann als Summe dieser standardisierten Differenzen über den gesamten Beobachtungszeitraum:

    \begin{equation*} Z = \frac {\displaystyle \sum_{i=1}^n( o_i - E(O_i)) }{{\sqrt { \displaystyle \sum_{i=1}^n Var (O_{i}})}} \end{equation*}

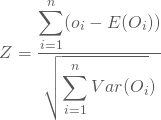
Für Dein Beispiel erhältst Du also Z = 2,035.

Unter der Nullhypothese ist Z approximativ standardnormalverteilt, und Du verwirfst die Nullhypothese einseitig, falls Z größer als der kritische Wert zur Irrtumswahrscheinlichkeit \alpha ist.

Für Dein Beispiel hast Du den kritischen Wert mit z_{0,95} = 1,645 gegeben und Du verwirfst die Nullhypothese. Hochschulabsolventen, die das Angebot der Personalagentur in Anspruch nehmen, kommen signifikant schneller zum Vertragsschluss als andere.

Falls Dein Statistikprogramm einen p-Wert ausgibt, vergleichst Du diesen mit Deinem \alpha. Mit p < \alpha verwirfst Du die Nullhypothese, anderenfalls behältst Du sie bei.