Wilcoxon-Mann-Whitney-Test / U-Test / Rangsummentest

Wilcoxon-Mann-Whitney-Test / U-Test / Rangsummentest

  • 21. März 2017
  • Posted by: Mika
Keine Kommentare

Der Wilcoxon-Mann-Whitney-Test, der auch unter verschiedenen anderen Namen bekannt ist, ist ein nichtparametrisches Verfahren. Er testet zwei unabhängige Stichproben auf Gleichheit Ihrer Lageparameter (Mittelwert bzw. Median). Damit ist er ist eine effiziente Alternative zum t-Test, wenn dessen Voraussetzungen nicht erfüllt sind.

Voraussetzungen für den Wilcoxon-Mann-Whitney-Test

Du kannst ihn auf die unabhängigen Stichproben zweier mindestens ordinalskalierter Zufallsvariablen X und Y anwenden. Ihm liegt folgende Idee zugrunde: falls beide Stichproben die gleichen Lageparameter besitzen, so ist es für zwei zufällig von X und Y gezogene Beobachtungen gleich wahrscheinlich, dass die Beobachtung von X größer als die von Y ausfällt, wie es der umgekehrte Fall ist. Ist dagegen Median und/oder Mittelwert von X größer als der von Y, so ist es wahrscheinlicher, dass auch die zufällige Beobachtung von X größer ist als die von Y ist.

Aufstellen von Hypothesen

H_0: P(X>Y) = P(Y>X) gegen

H_1: P(X>Y) \ne P(Y>X) bzw. P(X>Y) > P(Y>X) oder P(X>Y) < P(Y>X)

Stell Dir vor, Dich interessiert ein Vergleich der Einstiegsgehälter von Hochschulabsolventen in Frankfurt (F) und in München (M). Dazu befragst Du eine Reihe von Testpersonen. Als Ergebnis erhältst Du das angegebenes monatliches Gehalt, der Größe nach geordnet. Diese sind in Zeile 1 und 2 der nachfolgenden Tabelle zu sehen. Zeile 3 enthält die aufsteigend geordneten Ränge. Falls zwei gleiche Werte auftauchen, was hier nicht der Fall ist, müsstest Du „mitteln“: Angenommen, Platz 7 und 8 wären mit dem gleichen Wert belegt, erhielten beide den Wert 7,5.

1 Gehalt in € 1550 1900 2200 2375 2400 2500 2700 3200 3350 3500 3950 4900 U-Wert
2 Stadt F F M M F F F F M M F M
3 Rang 1 2 3 4 5 6 7 8 9 10 11 12
4 Anzahl von Rängen kleiner als M 2 2 6 6 7 23
5 Anzahl von Rängen kleiner als F 0 0 2 2 2 2 4 12
6 R_M=12+10+9+4+3=38 R_F=11 + 8 + 7 + 6 +5+2+1=40
7 n_M=5 n_F=7

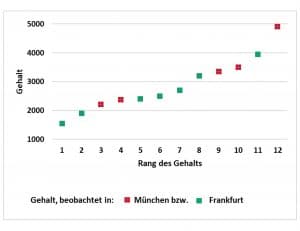
Die Grafik zeigt ebenfalls das Ergebnis Deiner Befragung:

Zur Durchführung des Tests bestimmst Du zunächst die U-Werte für beide Variablen (hier: Städte). Diese geben an, wie viele Rangwerte der anderen Variablen insgesamt niedriger sind. Dabei kannst Du auf zwei Arten vorgehen.

Für kleine Stichproben von Hand

Du beginnst mit dem größten Rangwert aller Beobachtungen, stellst fest, zu welcher Variablen er gehört und zählst, wie viele Beobachtungen der anderen Variablen im Rang kleiner sind als er. Das wiederholst Du für alle Werte der ersten Variablen und summierst. Das größte beobachtete Gehalt wurde in München beobachtet. Es gibt 7 Gehaltsnennungen aus Frankfurt, die niedriger sind. Zu den beiden nächstgroßen Gehaltsangaben aus München gibt es jeweils 6 Nennungen aus Frankfurt, deren Rang niedriger ist, usw.

Die Summe dieser Werte ergibt U_M = 23, siehe Zeile 4 der Tabelle. Das zweithöchste Gehalt, das angegeben wurde, stammt aus Frankfurt. Es gibt vier Gehaltsangaben aus München, die darunter liegen. Die beiden niedrigsten Gehaltsangaben stammen aus Frankfurt. Zu Ihnen gibt es keine Nennungen aus München, die niedriger sind. U_F=12 ergibt sich in Zeile 5 der Tabelle durch Summierung dieser Werte.

Für große Stichproben per Formel

Du bestimmst die aufsteigend geordneten Ränge der Beobachtungen beider Variablen zusammen (Zeile 3 der Tabelle) und vermerkst dabei zu welcher Variablen sie gehören. Dann berechnest Du die Summe der Rangplätze, die auf beide Variablen entfallen, zu R_M=38 und R_F=40 (Zeile 6 der obigen Tabelle). n_M und n_F sind die Anzahl der Beobachtungen. Dann ergeben sich die U-Werte durch

    \begin{equation*} U_M=R_M - \frac {n_M \cdot (n_M + 1)} 2 = 38 - \frac {6 \cdot 6} 2 = 23 \end{equation*}

und

    \begin{equation*} U_F=R_F - \frac {n_F \cdot (n_F + 1)} 2 = 40 - \frac {7 \cdot 8} 2 = 12 \end{equation*}

Der kleinere der beiden U-Werte ist Deine Prüfgröße.

    \begin{equation*} U_{pr} = min (U_M,U_F) = min(12;23) = 12 \end{equation*}

Die exakten kritischen Werte liegen für den zweiseitigen Test zum Niveau von 5\% so tabelliert vor, dass unter der Nullhypothese und bei gegebenen Stichprobengrößen gilt:

    \begin{equation*} P(U \ge U_{kr}| H_0;n_M,n_F) = 5 \% \end{equation*}

Du verwirfst die Nullhypothese, wenn U{pr} kleiner als U{kr} ist.
Im obigen Beispiel lautet Deine zweiseitige Testentscheidung:

    \begin{equation*} U_{pr} = 12 > 5 = U_{kr}(5;7) \end{equation*}

und die Nullhypothese, die Gehälter seien in beiden Städten gleich, kann nicht verworfen werden.

Für n_M >3, n_F >3, und (n_M+n_F)>19 ist U approximativ normalverteilt mit

    \begin{equation*} m_U = \frac {n_M \cdot n_F} 2 \quad und \quad \sigma_U = \sqrt {\frac {n_M \cdot n_F \cdot (n_M + n_F +1)} {12}}.\end{equation*}

Die Formulierung von Wilcoxon lautet etwas anders, kommt aber zum gleichen Ergebnis.

Der Wilcoxon-Mann-Whitney-Test benötigt lediglich ordinalskalierte Daten und keine Verteilungsannahme. Damit greift er, wenn die Voraussetzungen für die Anwendung des t-Tests nicht gegeben sind; sind sie erfüllt, beträgt seine Effizienz im Vergleich mit dem t-Test immerhin 95\%, wobei er robuster gegenüber Ausreißern ist.