Chi-Quadrat-Unabhängigkeitstest

Chi-Quadrat-Unabhängigkeitstest

  • 18. November 2016
  • Posted by: Mika
Keine Kommentare

Hast Du eine Stichprobe mit den Merkmalwerten zweier beliebig skalierter Zufallsvariablen erhoben, so kannst Du mit dem Chi-Quadrat-Unabhängigkeitstest testen, ob diese Zufallsvariablen stochastisch unabhängig sind. Du kannst also prüfen, ob das Auftreten einer Merkmalsausprägung der ersten Variablen nicht davon beeinflusst wird, welche Ausprägung die andere Variable annimmt und umgekehrt.

Stochastische Unabhängigkeit als Voraussetzung für viele statistische Modelle

Stell Dir vor, Du hast beispielsweise eine Untersuchung des Ausgabeverhaltens von Studenten in Deutschland mit dem Umfang n=200 durchgeführt und dabei unter anderem die Zufallsvariablen X: „Geschlecht“ und Y: „durchschnittliche monatliche Ausgaben für Nahrungsmittel“ erhoben. Als nächstes möchtest Du testen, ob diese Variablen unabhängig voneinander sind, ob also Männer und Frauen das gleiche Ausgabeverhalten für Nahrungsmittel aufweisen, oder ob es systematische Unterschiede gibt.

Deine Hypothesen lauten:

H_0: die Zufallsvariablen „Geschlecht“ und „durchschnittliche monatliche Ausgaben für Nahrungsmittel“ sind stochastisch unabhängig voneinander.

H_1: die Zufallsvariablen „Geschlecht“ und „durchschnittliche monatliche Ausgaben für Nahrungsmittel“ weisen Abhängigkeiten auf.

Aus Deiner Stichprobe erstellst Du folgende Tabelle, bei der Du zeilenweise die Probanden in die Merkmalsausprägungen X_1: Frauen und X_2: Männer unterteilst und in den Spalten das quantitativ-stetige Merkmal „Ausgaben für Nahrungsmittel“ in Klassen Y_1 bis Y_4 einteilst. Dabei spielt es keine Rolle, ob die Klassenbreiten unterschiedlich ist, wichtig ist nur, dass später alle erwarteten Klassenhäufigkeiten größer als 5 sind:

Y: „Durchschnittliche Ausgaben für Nahrungsmittel“
X: „Geschlecht“ 150-250 250-300 300-350 über 350 Summe Rel. Häufigkeit
Y_1 Y_2 Y_3 Y_4 n_{i \cdot } h_{i \cdot }
Frauen X_1 17 33 35 10 95 0,475
Männer X_2 9 32 47 17 105 0,525
Summe n_{\cdot j} 26 65 82 27 200 1
Rel. Häufigkeit h_{\cdot j} 0,13 0,325 0,41 0,135 1

Häufigkeiten und Randhäufigkeiten

Im Inneren der Tabelle hast Du die Häufigkeiten n_{ij} eingetragen, als Häufigkeiten, mit denen die Kombination aus Merkmal X_i und Y_j in Deiner Stichprobe auftritt, sowie die Randhäufigkeiten n_{i \cdot } für die Gesamthäufigkeit der Merkmalsausprägung X_i und n_{\cdot j} für die Gesamthäufigkeit der Merkmalsausprägung Y_j.

An den Rändern der Tabelle berechnest Du dann die relativen Häufigkeiten h_{i\cdot }=\frac{n_{i\cdot}}{n} und h_{\cdot j }=\frac{n_{\cdot j}}{n} , die angeben, welcher Anteil der Stichprobe auf die verschiedenen Merkmalsausprägungen der jeweiligen Variablen entfällt.

Falls die Nullhypothese gilt, sind die beiden Zufallsvariablen X und Y stochastisch unabhängig voneinander. Dann sind die Wahrscheinlichkeiten für das Auftreten der X_i nicht davon abhängig, welches Y_j eintritt, und umgekehrt. Die bedingten Wahrscheinlichkeiten sind dann gleich den Einzelwahrscheinlichkeiten:

    \begin{equation*} P (X_i | Y_j) = P(X_i) \quad und \quad P(Y_j|X_i) = P(Y_j),\quad f\"ur\quad beliebige \quad i,j \end{equation*}

Dann lassen sich die Wahrscheinlichkeit p_{ij} für das Auftreten der Kombination der Merkmalsausprägungen X_i und Y_j als Produkt der Einzelwahrscheinlichkeiten zerlegen:

    \begin{equation*} p_{ij }= P[(X_{i}) und (Y_{j})] = {P(X_{i})} \cdot {P(Y_{j})}} \end{equation*}

Geschätzte Wahrscheinlichkeiten

Als Schätzwerte für p_{ij} werden die Produkte der relativen Randhäufigkeiten h_{i \cdot}∙ und h_{\cdot j} verwendet. Damit wird zum Beispiel die unter der Nullhypothese erwartete Häufigkeit, dass ein zufällig ausgewählter Student weiblich ist und 250 bis 300 Euro pro Monat für Nahrungsmittel ausgibt, wie folgt berechnet:

    \begin{equation*} n \cdot p_{12 }= n \cdot h_{1 \cdot} \cdot h_{\cdot 2} = 200 \cdot 0,475 \cdot 0,325 = 30,875 \end{equation*}

Beim Chi-Quadrat-Unabhängigkeitstest vergleichst Du nun die Häufigkeiten n_{ij} Deiner Stichprobe mit den unter der Nullhypothese erwarteten Häufigkeiten n∙\cdot p_{ij}.

Teststatistik beim Chi-Quadrat-Unabhängigkeitstest

Für die Teststatistik quadrierst Du diese Differenzen, normierst sie mit den erwarteten Häufigkeiten und addierst über alle Merkmalsausprägungen von X und alle von Y:

    \begin{equation*} \chi^2 = \displaystyle \sum_{i=1} ^m \displaystyle \sum_{j=1} ^n \frac{(n_{ij} - n \cdot p_{ij })^2}{n \cdot p_{ij}} \end{equation*}

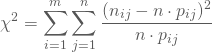
Die Teststatistik wird auch Chi-Quadrat-Koeffizient genannt und folgt einer \chi^2-Verteilung mit (m-1) \cdot (n-1) Freiheitsgraden. Daher vergleichst Du ihren Wert mit dem der \chi^2-Verteilung zum Niveau (1-\alpha) = 95\% bei (2-1)∙(4-1)=3 Freiheitsgraden:
Mit

    \begin{equation*} 5,56 = \chi^2_{pr} < \chi^2_{kr} = 7,81 \end{equation*}

kannst Du die Nullhypothese für Dein Beispiel mit einer Irrtumswahrscheinlichkeit von 5 \% nicht verwerfen. Die Daten deuten also auf keinen systematischen Zusammenhang zwischen dem Geschlecht und dem Ausgabeverhalten bei Nahrungsmitteln hin.

Den Chi-Quadrat-Test darfst Du nur anwenden, wenn alle erwarteten Häufigkeiten größer als 5 sind. Bei einem quantitativ-stetigen Merkmal kannst Du diese Voraussetzung oft dadurch erfüllen, dass Du die Klassen verbreiterst.