Häufigkeiten (absolute, relative, kumulierte)

Hast Du Daten zu einem diskreten Merkmal mit k verschiedenen Ausprägungen gegeben, so möchtest Du für eine erste Übersicht meist wissen, wie oft die verschiedenen Ausprägungen in Deiner Erhebung beobachtet werden.

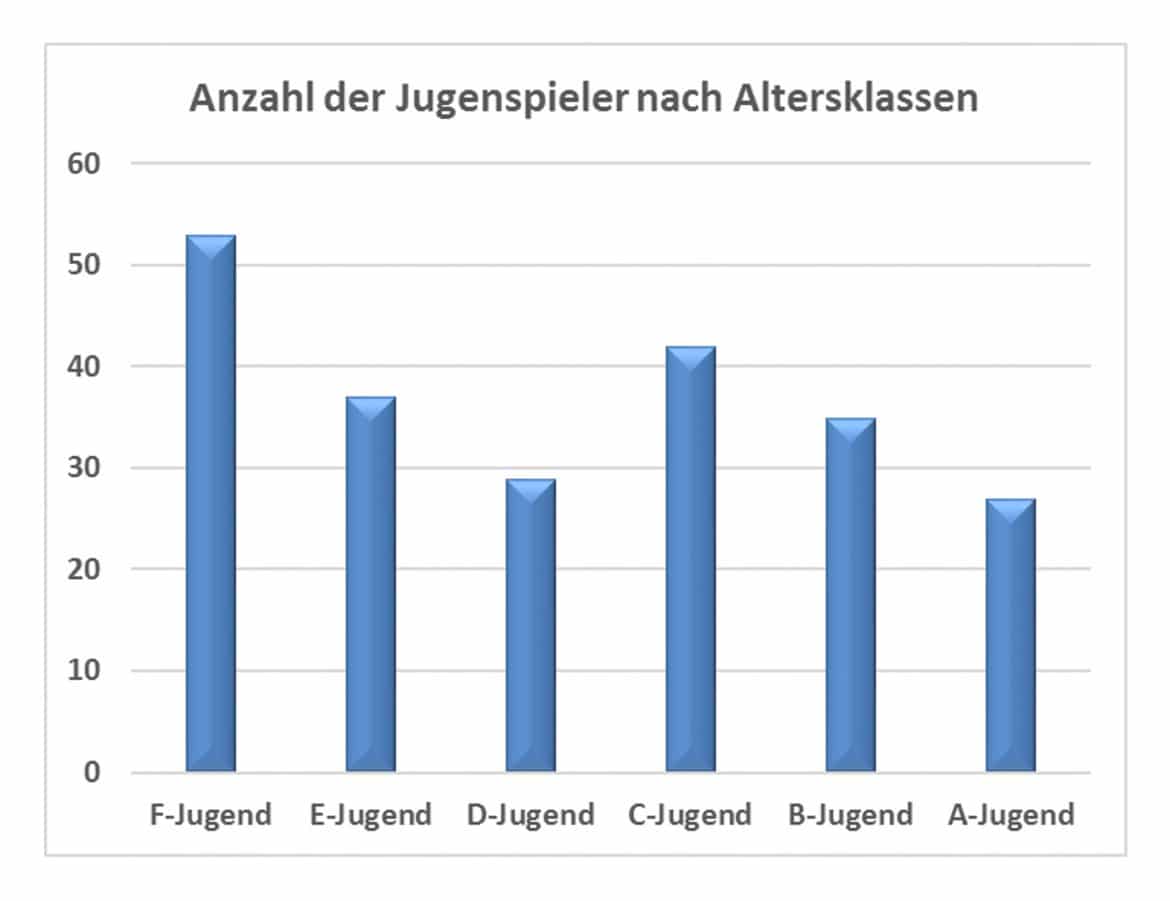
Als Jugendvorstand des Sportvereins SV Kaiserhof interessiert es Dich zum Beispiel, wie sich Deine Vereinsmitglieder auf die verschiedenen Altersgruppen, beginnend mit den jüngsten Spielern in der der F-Jugend bis zu den ältesten Jugendlichen in der A-Jugend verteilen.

Ein Blick in die Mitgliederdatei ergibt die absoluten Häufigkeiten der dritten Tabellenspalte:

Häufigkeiten:		absolute H.	relative H.	kumulierte H.
i	Jugendgruppe			F_i
1	F-Jugend	53	0,2377	0.2377
2	E-Jugend	37	0,1659	0,4036
3	D-Jugend	29	0,1300	0,5336
4	C-Jugend	42	0,1883	0,7220
5	B-Jugend	35	0,1570	0.8789
6	A-Jugend	27	0,1211	1,0000
Summe		223	1,0000

Wie kommt man auf die Werte?

Die absoluten Häufigkeiten geben also die Anzahl der Vereinsmitglieder an, die zu der i-ten Jugendgruppe gehören; in der F-Jugend beispielsweise sind 53 Spieler angemeldet, in der A-Jugend etwa sind es nur 27. Die Summe dieser Werte ergibt folglich die Gesamtzahl n der Mitglieder.

Dividierst Du die absolute Häufigkeite durch die Gesamtzahl n der Beobachtungen, so erhältst Du die relative Häufigkeit in der vierten Tabellenspalte:

   

Die geben die Anteile der Vereinsmitglieder an, die zu den verschiedenen Jugendgruppen gehören. Multipliziert mit 100 erhältst Du die prozentualen Anteile, die auf die verschiedenen Gruppen entfallen. So beträgt in Deinem Beispiel der Anteil der E-Jugend-Spieler an allen Jugendlichen des Vereins zum Beispiel 0,1659 oder , der der A-Jugend-Spieler 0,1211 oder .

Möchtest Du außerdem wissen, wie viele Vereinsmitglieder etwa in den Altersgruppen bis zur C-Jugend angemeldet sind, so benötigst Du die kumulierten relativen Häufigkeiten. Für die i-te Altersgruppe erhältst Du sie durch Summieren der Anteile aller jüngeren oder gleichaltrigen Klassen:

   

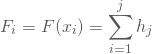
Die kumulierten relativen Häufigkeiten sind in der fünften Tabellenspalte gegeben. In den Altersklassen bis zur D-Jugend befinden sich also der Jugendspieler; Du erhältst den Wert, indem Du die Anteile der F-Jugend, E-Jugend und D-Jugend addierst.

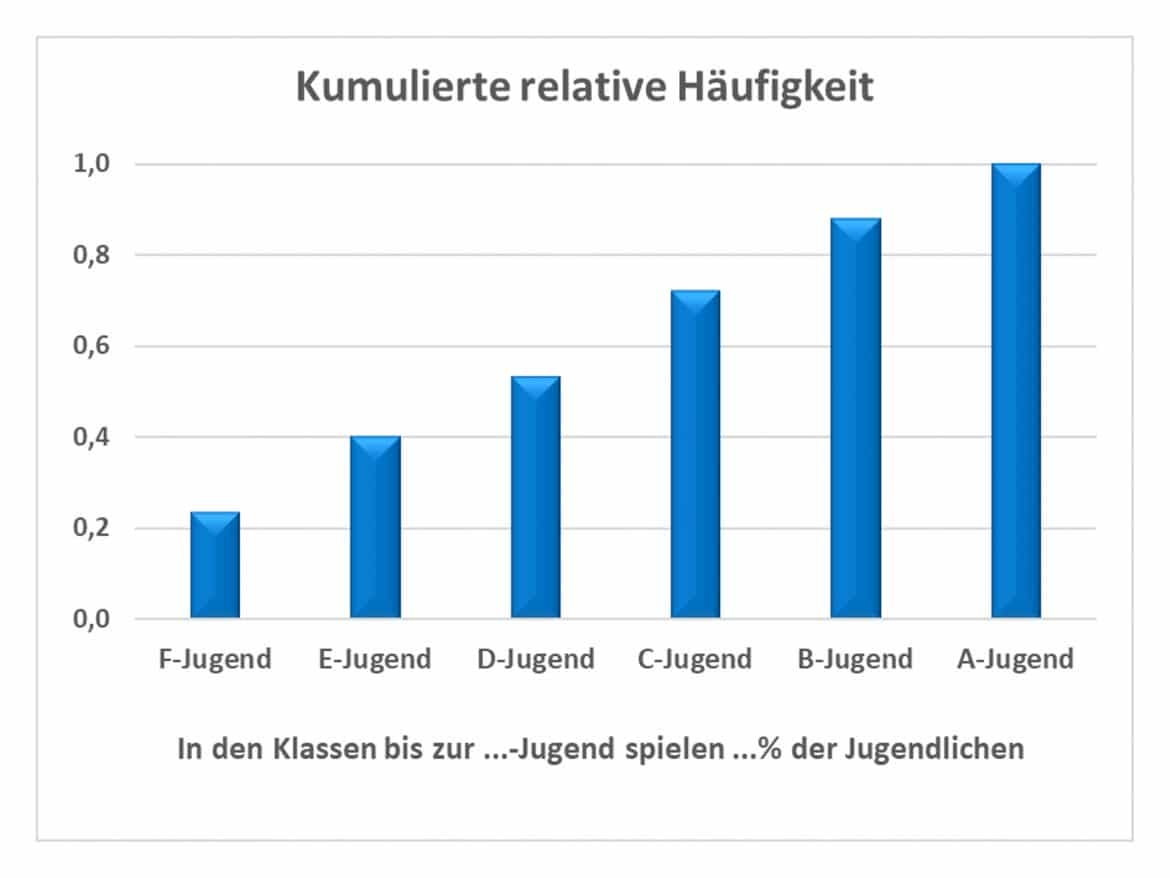Die kumulierten relativen Häufigkeiten werden auch als empirische Verteilungsfunktion Deiner Erhebung bezeichnet. Für Ihre Bestimmung ist mindestens Ordinalskalenniveau Deiner Daten erforderlich.

Du kannst absolute, relative und kumulierte Häufigkeiten wie hier für ein Merkmal ermitteln; man spricht dann von eindimensionalen Häufigkeiten. Hast Du mehrere Merkmale erhoben und betrachtest die Häufigkeiten der möglichen Ausprägungskombinationen Deiner Daten, so arbeitest Du mit mehrdimensionalen Häufigkeiten.