Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Standardabweichung
- 7. September 2017
- Posted by: Mika
Formal erhältst Du die Standardabweichung ![]() als positive Quadratwurzel aus der empirischen Varianz. Diese ist der Quotient aus den über alle Beobachtungswerte summierten quadratischen Abweichungen der Beobachtungswerte von ihrem Mittelpunkt und der Anzahl der Beobachtungswerte:
als positive Quadratwurzel aus der empirischen Varianz. Diese ist der Quotient aus den über alle Beobachtungswerte summierten quadratischen Abweichungen der Beobachtungswerte von ihrem Mittelpunkt und der Anzahl der Beobachtungswerte:
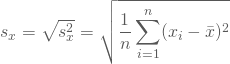
Unterschied zur Varianz
Die Quadrierung der Abstände bei der Konstruktion der Varianz bewirkt, dass der Einfluss größerer Abweichungen und damit auch der von Ausreißern verstärkt eingeht; die Maßeinheit der Varianz entspricht dadurch aber nicht mehr der der Beobachtungswerte sondern dem Quadrat deren Maßeinheit, was ihre Größe schwer interpretierbar macht.
Die Maßeinheit der Standardabweichung entspricht dagegen wieder der der Beobachtungswerte. Dadurch ist sie anschaulich besser mit dem Begriff der Streuung vereinbar und kann als mittlere Abweichung oder durchschnittlicher Fehler interpretiert werden.
Ein Sägewerk schneidet Bretter der Länge 100 Zentimeter zu. Ein sehr genauer Kunde misst 6 Bretter seiner Lieferung nach und erhält die folgenden Längen:
| lfd. Nummer | 1 | 2 | 3 | 4 | 5 | 6 | |
| Länge in cm
|
99,8 | 99,5 | 100,1 | 99,2 | 100,5 | 100,8 | 99,983 |
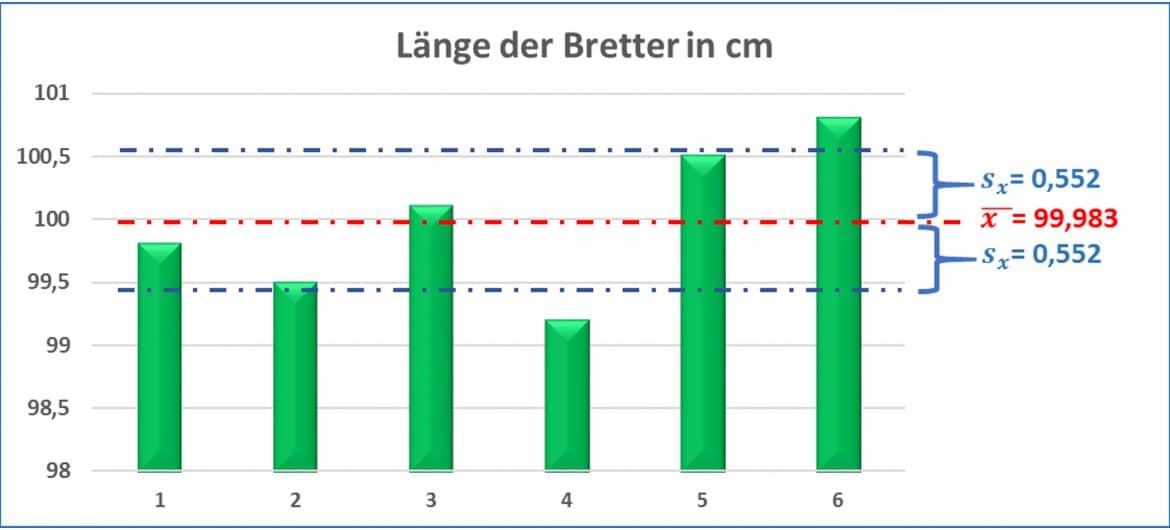
Der Mittelwert von 99,983 scheint zunächst ein recht gutes Ergebnis zu sein. Jetzt berechnet der Kunde als Streuungsmaß die Standardabweichung:
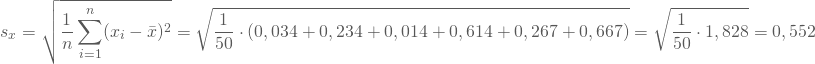
Die Standardabweichung von ![]() besagt, dass die Brettlängen im Mittel um 0,552 cm um den Mittelwert herum streuen. Je nach Verwendungszweck der Bretter könnte das zu viel sein und die Lieferung sollte zurückgegeben werden.
besagt, dass die Brettlängen im Mittel um 0,552 cm um den Mittelwert herum streuen. Je nach Verwendungszweck der Bretter könnte das zu viel sein und die Lieferung sollte zurückgegeben werden.
