ROC-Kurve

ROC-Kurve

  • 19. Juni 2017
  • Posted by: Mika
Keine Kommentare

Die ROC-Kurve (Receiver-Operating-Characteristics) vermittelt Dir einen Überblick über die diagnostische Qualität eines Tests, mit dem Du eine Ja/Nein-Entscheidung fällst, in Abhängigkeit vom gewählten Parameter.

Stell Dir vor, Du arbeitest in der Zentralen Vergabestelle für Studienplätze und arbeitest an der Entscheidungsregel, mit der die Bewerber zum Medizinstudium als geeignet oder nicht geeignet klassifiziert und entsprechend zum Studium zugelassen werden.

Dabei kannst Du verschiedene Wertungen von Abiturnoten, Begabung, Neigung, … einsetzen. Natürlich möchtest Du das Konzept verwenden, das die wenigsten Fehlentscheidungen bewirkt. Für Deine Entscheidung kannst Du auf umfangreiches Datenmaterial zurückgreifen.

Zwei Arten von richtigen Beurteilungsmöglichkeiten

  • In 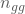n_{gg} Fällen führt Deine Beurteilung dazu, dass Du einen geeigneten Bewerber (g) als geeignet (g) erkennst, sowie
  • in 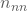n_{nn} Fällen führt Deine Beurteilung dazu, dass Du einen ungeeigneten Bewerber (n) als nicht geeignet (n) aussortierst.
  • Daneben kannst Du zwei Beurteilungen treffen, die zu Fehlentscheidungen führen:
  • In 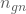n_{gn} Fällen führt Deine Beurteilung dazu, dass Du einen geeigneten Bewerber (g) als nicht geeignet (n) aussortierst.
  • In 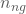n_{ng} Fällen führt Deine Beurteilung dazu, dass ein ungeeigneter Bewerber (n) als geeignet (g) zugelassen wird.

Die Tabelle stellt die verschiedenen Möglichkeiten gegenüber.

Bewerber werden als … erklärt

Bewerber sind für die Einstellung …..

 als geeignet erklärt

g

 als nicht geeignet erklärt

n

 Summe
de facto geeignet g n_{gg} n_{gn} n_{\cdot g}
de facto nicht geeignet n n_{ng} n_{nn} n_{\cdot n}
Summe n_{g \cdot} n_{n \cdot}

 

Interessant sind nun zwei Quotienten

  • Der Anteil der richtigen positiven Entscheidungen an der Gesamtzahl der de facto positiven. In Deinem Fall ist das der Quotient aus als zutreffend geeignet erklärten und de facto geeigneten zu den de facto geeigneten. Diesen Quotienten bezeichnet man als Sensitivität eines Tests.

        \begin{equation*} Sensitivit \"at : \quad \frac { n_{gg}} {n_{gg} + n_{gn} } = \frac{ n_{gg}} {n_{g \cdot}} \end{equation*}

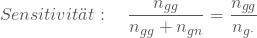
  • Der Anteil der richtigen negativen Entscheidungen an der Gesamtzahl der de facto negativen. In Deinem Beispiel dividierst Du die richtigerweise als nicht geeignet erklärten Personen durch die Anzahl der tatsächlich nicht geeigneten. Dieser Quotient wird auch Spezifität eines Tests genannt.

        \begin{equation*} Spezifit\"at : \quad \frac { n_{nn}} {n_{nn} + n_{ng} } =\frac { n_{nn}} {n_{n \cdot} }\end{equation*}

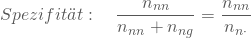
Aus den Erfahrungen der vergangenen Jahre, in denen immer wieder verschiedene Testkonzeptionen verwendet wurden, erstellst Du die folgende Tabelle:

Testkonzept Sensitivität Spezifität
A 0,2 0
B 0,4 0,1
C 0,6 0,2
D 0,8 0,35
E 0,9 0,5
F 1 1

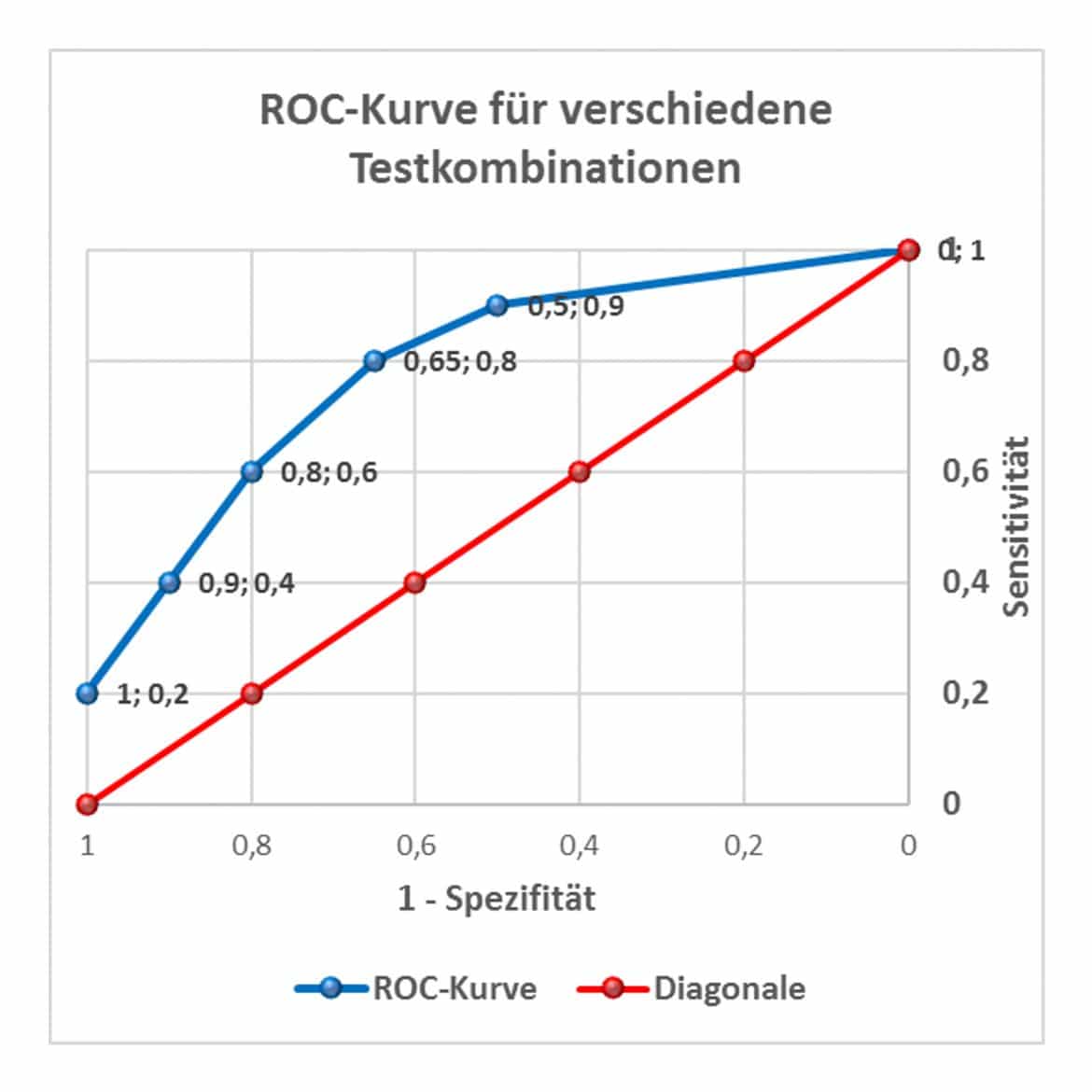
Die ROC-Kurve visualisiert Dir Sensitivität und das Komplement zur Spezifität des jeweiligen Test. Läge ein Punkt in der linken oberen Ecke des Diagramms, in dem Spezifität und Sensitivität des Tests eins betragen, wäre dieser Test optimal. Denn dann würdest Du mit diesem Test keine Fehlentscheidungen treffen. Er ist aber leider nur von theoretischem Interesse.

Die rote Diagonale stellt Entscheidungen auf reiner Zufallsbasis dar.

Die blaue Linie stellt die Werte Deiner Tabelle dar. Sie liegt durchgängig oberhalb der Diagonalen, so dass alle betrachteten Testverfahren besser sind als eine zufällige Entscheidung. Du solltest Dich für das Konzept entscheiden, dessen Abstand zur oberen linken Diagrammecke am geringsten ist.

Hier liegt der Test C mit Sensitivität von 0,6 und Spezifität von 0,2 (1 – Spezifität = 0,8) am dichtesten an der oberen linken Ecke: ihm solltest Du den Vorzug geben.

ROC-Kurve

Auch noch gut zu wissen

Die ROC-Kurve stammt aus der Nachrichtentechnik, daher auch ihr ungewöhnlicher Name.

Problematisch für ihre Anwendung in Fällen wie hier ist sicherlich die Erhebung der für die Berechnung der Quotienten erforderlichen Daten. Während sich in Deinem Beispiel die irrtümlich als geeignet klassifizierten Studenten im Laufe des Studiums als ungeeignet herausstellen, ist es praktisch unmöglich, die Anzahl derjenigen, die irrtümlich als ungeeignet beurteilt wurden, zu ermitteln.