Symmetrische Verteilung

Eine symmetrische Verteilung ist ein Spezialfall einer Wahrscheinlichkeitsverteilung. Genauer gesagt, heißt eine Verteilung symmetrisch und einen Wert a, wenn für jede Realisation x der Zufallsvariablen X die folgende Gleichheit gilt:

   

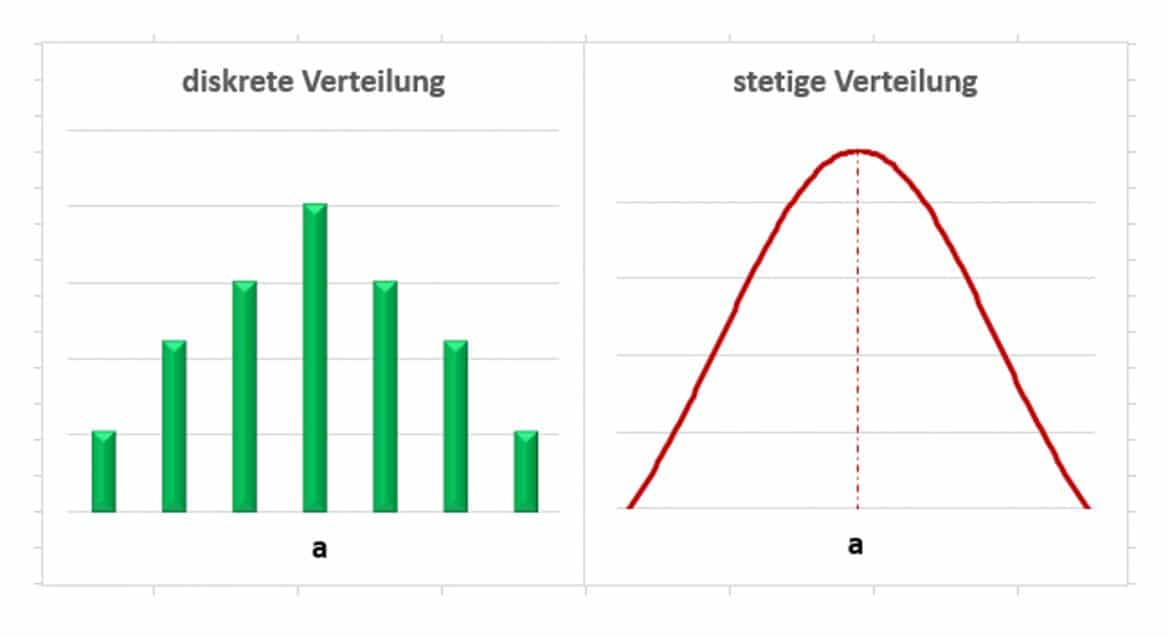
Grafische Veranschaulichung der Symmetrie-Eigenschaft

Die linke Grafik gehört zu einer diskreten symmetrischen Verteilung und zeigt ihre Wahrscheinlichkeitsfunktion. Im Gegensatz dazu zeigt die rechte Grafik die Dichtefunktion einer stetigen Verteilung. In beiden Fällen kannst Du ihre Symmetrie in spiegelverkehrtem Verlauf der Funktionen um den Symmetriepunkt a herum erkennen:

Nimmt a den Wert null an, so liegt die Verteilung symmetrisch um den Nullpunkt und es gilt:

   

Oft betrachtest Du Verteilungen, die symmetrisch um den Erwartungswert liegen. Das wahrscheinlich wichtigste Beispiel für eine symmetrische Verteilung ist die Normalverteilung, auch Gaußverteilung genannt. Aber auch die Gleichverteilung oder die Laplace-Verteilung sind beispielsweise symmetrisch. Nicht symmetrische stetige Verteilungen sind zum Beispiel die Lognormalverteilung, die Exponentialverteilung, die Weibull-Verteilung, die Gamma-Verteilung, die Beta-Verteilung. Nichtsymmetrische diskrete Verteilungen sind zum Beispiel die Multinomialverteilung, die Poissonverteilung, die geometrische Verteilung oder die hyptergeometrische Verteilung. Manche Verteilungen haben sowohl symmetrische als auch nichtsymmetrische Varianten, wie zum Beispiel die Binomialverteilung,