Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Laplace-Verteilung
- 16. April 2018
- Posted by: Mika
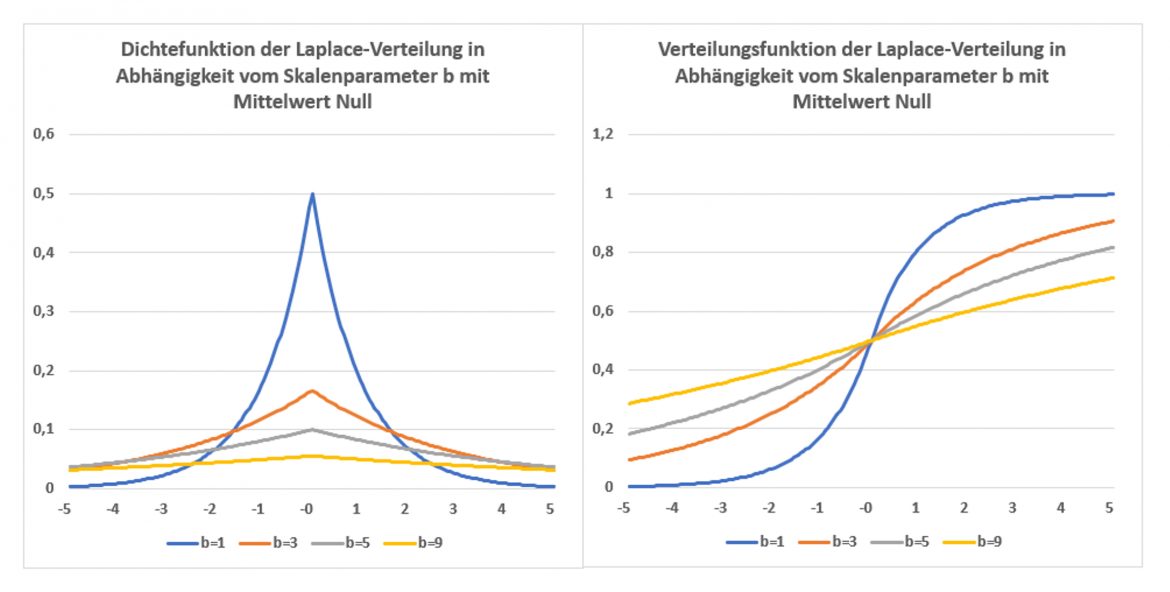
Die Laplace-Verteilung ist eine stetige symmetrische Verteilung mit dem Lageparameter ![]() und außerdem einem Skalenparameter b, der die Steilheit der Dichtefunktion angibt. Wie die linke Grafik zeigt, besitzt die Dichtefunktion im Bereich des Mittelwerts einen spitzen Verlauf und läuft zudem zu den Enden hin flach aus. Wegen ihres Aussehens wird die Laplace-Verteilung auch doppelte Exponentialverteilung genannt. Die rechte Grafik zeigt die entsprechenden Verteilungsfunktionen.
und außerdem einem Skalenparameter b, der die Steilheit der Dichtefunktion angibt. Wie die linke Grafik zeigt, besitzt die Dichtefunktion im Bereich des Mittelwerts einen spitzen Verlauf und läuft zudem zu den Enden hin flach aus. Wegen ihres Aussehens wird die Laplace-Verteilung auch doppelte Exponentialverteilung genannt. Die rechte Grafik zeigt die entsprechenden Verteilungsfunktionen.
Kennzahlen der Laplaceverteilung
Die Dichtefunktion der Laplaceverteilung ist durch
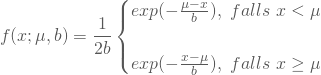
gegeben, die zugehörige Verteilungsfunktion erhältst Du zudem durch Integration mit dem folgenden Ergebnis:
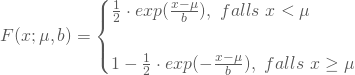
Für ![]() und
und ![]() entspricht ihr aufsteigender Ast exakt der Exponentialverteilung.
entspricht ihr aufsteigender Ast exakt der Exponentialverteilung.
Du erhältst Mittelwert und Varianz der Laplace-Verteilung wie folgt:
![]()
Ein Beispiel für die Anwendung der Laplace-Verteilung sind logarithmierte Änderungsraten des Zinssatzes auf Staatsanleihen im Zeitverlauf. Die beobachtete Verteilung kann man in diesem Fall gut durch die Laplaceverteilung wiedergeben.
