Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Erwartungstreue
- 16. November 2016
- Posted by: Mika
Du möchtest Deine Stichprobe nutzen, um die unbekannten Parameter der Grundgesamtheit zu schätzen. Dafür ist die Eigenschaft der Erwartungstreue ein wichtiges Kriterium bei der Auswahl geeigneter Schätzfunktionen. Sie besagt, dass der theoretische Erwartungswert der Schätzfunktion mit dem Erwartungswert der Zufallsvariablen in der Grundgesamtheit übereinstimmen sollte.
Beispielberechnung Erwartungstreue
Stell Dir vor beispielsweise vor, Du arbeitest für ein Pharmaunternehmen, das ein Medikament „Schmerzade“ mit einer angegebenen Wirkstoffmenge von 10 mg anbietet. Weiterhin stellt dieses täglich 500.000 Dragees her. Deren tatsächliche jeweilige Wirkstoffmenge kannst Du als Realisation einer Zufallsvariablen X mit unbekanntem Mittelwert ![]() und unbekannter Varianz
und unbekannter Varianz ![]() betrachten. Denn neben der korrekten Einstellung der Maschinen wirken auch immer Zufallseinflüsse.
betrachten. Denn neben der korrekten Einstellung der Maschinen wirken auch immer Zufallseinflüsse.
Berechnung von Mittelwert und Stichprobenvarianz
Für die Kontrolle der Wirkstoffmenge entnimmst Du täglich eine Stichprobe vom Umfang n=200 und berechnest aus dieser Stichprobe wie gewohnt den Mittelwert und die Stichprobenvarianz.
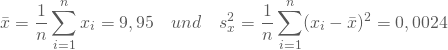
Theoretischer Erwartungswert
Die Elemente der Stichprobe sind eine Teilmenge der Grundgesamtheit. Dementsprechend sind sie natürlich Realisationen der Zufallsvariablen X mit gleichem unbekannten Mittelwert ![]() und gleicher unbekannter Varianz
und gleicher unbekannter Varianz ![]() der Grundgesamtheit. Also sind die für die Berechnung der Stichprobenparameter verwendeten Schätzfunktionen
der Grundgesamtheit. Also sind die für die Berechnung der Stichprobenparameter verwendeten Schätzfunktionen ![]() und
und ![]() als Funktionen von X auch wieder Zufallsvariablen. Sie wären somit geeignete Schätzfunktionen für
als Funktionen von X auch wieder Zufallsvariablen. Sie wären somit geeignete Schätzfunktionen für ![]() und
und ![]() in der Grundgesamtheit, falls ihr theoretischer Erwartungswert mit
in der Grundgesamtheit, falls ihr theoretischer Erwartungswert mit ![]() und
und ![]() übereinstimmte.
übereinstimmte.
Das kannst Du dadurch überprüfen, dass Du die Daten in die folgende Formel einsetzt: Mit
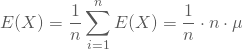
stellt der Mittelwert der Stichprobe eine erwartungstreue Schätzfunktion für den Mittelwert der Grundgesamtheit dar. Damit kannst Du Deinen berechneten Stichprobenmittelwert als erwartungstreue Parameterschätzung für das unbekannte ![]() der Grundgesamtheit nehmen:
der Grundgesamtheit nehmen:
![]()
Theoretische Varianz
Bei der Varianz sieht das anders aus:
![Rendered by QuickLaTeX.com \begin{equation*} E(S_X^2) &= \frac {1} {n} \sum_{i=1}^n E[(X_i - \bar X)^2]= \frac {1} {n} \sum_{i=1}^n E[(X_i - \mu + \mu - \bar X)^2] \end{equation*}](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-5453635f04f71a76725db2fdbbf394b9_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} &= {\frac {1} {n}} [ \sum_{i=1}^n E(X_i - \mu)^2 - n \cdot E(\bar X - \mu)^2 ] \end{equation*}](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-f5bb23f60d71645a14b557d0c88a317b_l3.png)
![]()
Der theoretisch erwartete Wert für die Stichprobenvarianz ist also um die Varianz des Stichprobenmittelwertes kleiner als die Varianz der Grundgesamtheit.
Um dies zu korrigieren, kannst Du aber den Schätzwert sehr einfach mit Hilfe des Bessel´schen Korrekturfaktors ![]() modifizieren und erhältst einen erwartungstreuen Schätzwert für die Varianz der Grundgesamtheit:
modifizieren und erhältst einen erwartungstreuen Schätzwert für die Varianz der Grundgesamtheit:
![Rendered by QuickLaTeX.com \begin{equation*} S^2 = \frac {1} {n-1} \cdot \sum_{i=1}^n E[(X_i - \bar X)^2]\end{equation*}](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-99cee9378d9f7a24eb135883fcbe1915_l3.png)
Für Dein Beispiel wäre demnach der korrigierte und erwartungstreue Schätzwert für die Varianz der Grundgesamtheit aus der Stichprobe
![]()
etwas größer als die der Stichprobe ![]() .
.
Zusammenfassen lässt sich sagen, dass je kleiner Du Deine Stichprobe wählst, umso größer ist die Varianz des Stichprobenmittelwertes und umso deutlicher wirkt sich der Bessel´sche Korrekturfaktor aus.
Zudem nähert sich eine erwartungstreue Schätzfunktion im Mittel an die exakte Schätzung des Parameters an.
Abschließend nennt man eine Schätzfunktion, die keine systematischen Abweichungen aufweist, auch unverzerrt oder unbiased.
