Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Generalisierte Momentenmethode (GMM)
- 16. November 2016
- Posted by: Mika
Die generalisierte Momentenmethode ist eine Verallgemeinerung der einfachen Momentenmethode. Letztere ist eins der ältesten Verfahren zur Schätzung von Parametern der Grundgesamtheit und sehr einfach durchzuführen, weist aber den Nachteil auf, dass einige ihrer Schätzfunktionen nicht erwartungstreu sind.
Die Momentenmethode schätzt die Parameter einer Verteilung, indem sie die theoretischen Momente (![]() ) und empirischen Momente (
) und empirischen Momente (![]() ) der Verteilung gleichsetzt. Dabei sind die theoretischen Momente Funktionen der unbekannten Parameter der Grundgesamtheit und die empirischen aus der Stichprobe direkt zu berechnen.
) der Verteilung gleichsetzt. Dabei sind die theoretischen Momente Funktionen der unbekannten Parameter der Grundgesamtheit und die empirischen aus der Stichprobe direkt zu berechnen.
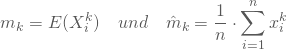
Einfache Momentenmethode: Beispielrechnung
Bei der einfachen Momentenmethode gehen so viele Momente in die Schätzfunktionen ein, wie Parameter zu schätzen sind. Dadurch ergibt sich ein lineares Gleichungssystem, dessen Lösung die Schätzungen für die wahren Parameter der Grundgesamtheit nach der Momentenmethode liefert, falls sie eindeutig ist.
Um beispielsweise die beiden Parameter einer Normalverteilung zu schätzen, werden die ersten beiden Momente ![]() und
und ![]() benötigt und es gilt:
benötigt und es gilt:
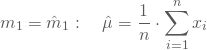
und
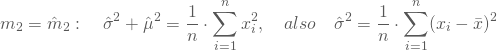
Generalisierte Momentenmethode: Beispielrechnung
Die generalisierte Momentenmethode verallgemeinert den Ansatz der einfachen Momentenmethode, indem sie zulässt, dass die Anzahl n der für die Schätzung verwendeten Momente größer sein kann als die Anzahl m der zu schätzenden Parameter.
Du legst zunächst fest, wie viele n Momente grundsätzlich für die Schätzung der m Parameter zugrundegelegt werden sollen. Jeder Parameter wird durch eine Funktion der Momente (![]() bis
bis ![]() ) geschätzt. Mit n > m ist das Gleichungssystem überbestimmt und kann nicht eindeutig gelöst werden.
) geschätzt. Mit n > m ist das Gleichungssystem überbestimmt und kann nicht eindeutig gelöst werden.
Als Beispiel kannst Du die Schätzfunktionen von ![]() und
und ![]() als Funktionen der ersten drei Momente
als Funktionen der ersten drei Momente ![]() bis
bis ![]() betrachten:
betrachten:
![]()
Mit diesem System hast du keine eindeutige Lösung gegeben, denn das Gleichungssystem ist überbestimmt. Du wählst nun die Schätzfunktionen für die unbekannten Parameter so, dass die Summe der quadratischen Abweichungen zwischen empirischen und theoretischen Momenten minimiert wird.
Mithilfe von numerischen Optimierungsverfahren erhältst Du als Lösung die generalisierten Momentenschätzer.
Die generalisierte Momentenmethode schließt eine Reihe anderer Schätzmethoden als Spezialfälle ein, so auch den IV-Estimator und die Maximum-Likelihood-Methode.
