Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Kovarianzanalyse/ANCOVA
- 26. Januar 2017
- Posted by: Mika
Dieser Artikel erklärt, wann eine Kovarianzanalyse (ANCOVA) zum Einsatz kommt. Mit einer Varianzanalyse kannst Du den Einfluss von ein oder mehreren nicht metrisch-skalierten unabhängigen Variablen auf eine abhängige metrisch-skalierte Variable auf Signifikanz untersuchen. Dazu teilst Du die Beobachtungen der abhängigen Variablen nach ihrer Gruppenzugehörigkeit zu den Ausprägungen der unabhängigen Variablen ein. Du vergleichst dann die Varianz der Beobachtungswerte innerhalb einer Gruppe mit der zwischen den Gruppen und schließt auf Signifikanz, wenn die Varianz zwischen den Gruppen deutlich größer als die innerhalb der Gruppen ist.
Variablen werden aber häufig durch einen Mix von metrisch und nicht-metrisch skalierten unabhängigen Variablen beeinflusst. Das Ergebnis Deiner Varianzanalyse kann daher durch eine bestehende lineare Abhängigkeit von einer metrischen Variablen beeinflusst werden.
Idee der ANCOVA
Dem trägt die Kovarianzanalyse Rechnung: Sie geht vom allgemeinen linearen Modell aus. Einerseits wird eine abhängige Variable Y durch die Effekte verschiedener Kategorien der nicht metrischen Einflussgrößen bestimmt. Andererseits wird sie durch eine lineare Abhängigkeit von der unabhängigen metrischen Variablen X, der Kovariablen, bestimmt.
Im einfachsten Fall mit einer nicht-metrischen unabhängigen Variablen ![]() und einer Kovariablen X lässt sich
und einer Kovariablen X lässt sich ![]() , die j-te Beoabachtung der Zufallsvariablen Y für die i-te Gruppe von
, die j-te Beoabachtung der Zufallsvariablen Y für die i-te Gruppe von ![]() ) durch
) durch
![]()
darstellen. Dabei ist
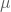 der Mittelwert von Y,
der Mittelwert von Y,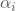 der Effekt der i-ten Kategorie von
der Effekt der i-ten Kategorie von 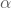 , mit
, mit 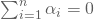 ,
,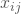 die j-te Realisation der unabhängigen Variablen X in der i-ten Gruppe,
die j-te Realisation der unabhängigen Variablen X in der i-ten Gruppe,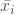 der Mittelwert der
der Mittelwert der 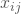 in der i-ten Gruppe
in der i-ten Gruppe- B die zu schätzende Koeffizientenmatrix für die lineare Abhängigkeit und
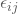 der (unbeobachtbare) j-te Störterm in der i-ten Gruppe.
der (unbeobachtbare) j-te Störterm in der i-ten Gruppe.
Ziel der ANCOVA
Ziel der Kovarianzanalyse ist es, den Einfluss der unabhängigen nicht-metrischen Variablen auf Signifikanz zu untersuchen, nachdem die Beobachtungen um den linearen Einfluss der Kovariablen (wie bei der Regressionsananalyse) bereinigt sind.
Stell Dir beispielsweise vor, Du als Regionalleiter einer Supermarktkette möchtest eine neuen Produktserie „Schneller Mittagstisch“ einführen. Dir stehen verschiedene Werbemittel zur Verfügung und Du möchtest wissen, ob deren Einsatz Deinen Umsatz signifikant beeinflussen kann. Außerdem weißt Du, dass neben dem Einfluss Deiner Werbung eine lineare Abhängigkeit vom Preis besteht.
Du entscheidest Dich, Deine Handlungsvarianten eine Woche lang an zehn Testmärkten auszuprobieren und zu dokumentieren, so dass Du je 20 Beobachtungen von Preis und abgesetzter Menge für jedes Werbemittel erhältst. Auf die erhaltenen Daten möchtest Du dann eine Kovarianzanalyse anwenden.
So könnte Deine Dokumentation aufgebaut sein:
| Lfd. Nummer | Umgesetzte Menge Y | Werbemittel
|
VK-Preis X |
|---|---|---|---|
| 1 | 27 | Sonderpräsentation | 4,50 € |
| 2 | 23 | Aktionstisch | 4,50 € |
| 3 | 24 | Zeitungsbeilage | 5,00 € |
| 4 | 16 | Aktionstisch | 4,70 € |
| 5 | 19 | Zeitungsbeilage | 4,30 € |
| … | … | … | … |
| 60 | 21 | Sonderpräsentation | 4,30 € |
Vorgehen bei einer ANCOVA
Bei der Kovarianzanalyse berechnest Du zuerst eine Regression der umgesetzten Menge Y auf die unabhängige metrische Variable Verkaufspreis und schätzt eine lineare Beziehung: Y = f(X).
Setzt Du in diese lineare Beziehung jeweils den Verkaufspreis ![]() , der bei der j-ten Beobachtung des i-ten Werbemittels gültig war, ein, so erhältst Du mit
, der bei der j-ten Beobachtung des i-ten Werbemittels gültig war, ein, so erhältst Du mit ![]() Schätzwerte für die preisbedingt umgesetzten Mengen. Subtrahierst Du diese von den abgesetzten Mengen
Schätzwerte für die preisbedingt umgesetzten Mengen. Subtrahierst Du diese von den abgesetzten Mengen ![]() , so erhältst Du bereinigte Werte
, so erhältst Du bereinigte Werte ![]() , die den nur durch die nicht-metrischen Variablen erklärten Teil der abgesetzten Menge darstellen.
, die den nur durch die nicht-metrischen Variablen erklärten Teil der abgesetzten Menge darstellen.
Auf diese ![]() führst Du dann eine Varianzanalyse durch, welche die durch die Gruppierung nach Werbemitteln erklärte Varianz mit der Restvarianz vergleicht. Du schließt auf signifikanten Einfluss der Werbemittel, falls dieser Quotient zu groß wird.
führst Du dann eine Varianzanalyse durch, welche die durch die Gruppierung nach Werbemitteln erklärte Varianz mit der Restvarianz vergleicht. Du schließt auf signifikanten Einfluss der Werbemittel, falls dieser Quotient zu groß wird.
Wie sieht die Prüfgröße aus?
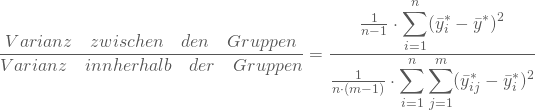
Dieser Quotient aus zwei ![]() -verteilten Variablen ist F-verteilt, mit (n-1) und (n⋅(m-1)) Freiheitsgraden. Du kannst durch den Vergleich mit dem kritischen F-Wert prüfen, ob der Einfluss der unabhängigen nicht-metrischen Variablen signifikant ist oder vernachlässigt werden kann.
-verteilten Variablen ist F-verteilt, mit (n-1) und (n⋅(m-1)) Freiheitsgraden. Du kannst durch den Vergleich mit dem kritischen F-Wert prüfen, ob der Einfluss der unabhängigen nicht-metrischen Variablen signifikant ist oder vernachlässigt werden kann.
Für Dein Beispiel mit n = 3 Werbemitteln und m = 20 Beobachtungen pro Werbemittel habe sich ein Prüfwert von ![]() ergeben. Damit entscheidest Du:
ergeben. Damit entscheidest Du:
![]()
und schließt auf signifikanten Einfluss der Werbemittel bei einer Irrtumswahrscheinlichkeit von ![]() .
.
Wann verwirfst Du die Nullhypothese?
Im Falle, dass Dein Programm den p-Wert ausgibt, kannst Du Deine Testentscheidung noch einfacher treffen. Du verwirfst dann die Nullhypothese, falls der ausgegebene p-Wert kleiner ist als Dein Niveau ![]() ist.
ist.
Die Kovarianzanalyse ist damit ein vielseitiges Analyseelement, das aber nur unter relativ engen Voraussetzungen angewandt werden darf, die im Vorfeld zu prüfen sind:
| Voraussetzung | Möglicher Test |
|---|---|
| Die abhängige Variable und die Kovariable sind in der Grundgesamtheit normalverteilt. | z. B. Anderson-Darling-Test |
| Es gibt einen linearen Zusammenhang zwischen der abhängigen Variablen und der Kovariablen. | F-Test auf Signifikanz der Regressionskoeffizienten |
| Die Varianz der Grundgesamtheit ist homogen | z. B. F-Test oder Bartlett-Test auf Homoskedastizität |
| Die lineare Regression ist in den verschiedenen Ausprägungen der unabhängigen nicht-metrischen Variablen homogen. | Dayton-Test |
